ПРИМЕНЕНИЕ ТЕОРИИ ХАОСА В ОБЛАСТИ КОДИРОВАНИЯ И ПЕРЕДАЧИ ИНФОРМАЦИИ

Воронцов И.И.

Самарский Государственный Технический Университет

Abstract - The article demonstrates the alternative cryptografy algorithm based on the last invesigatons in the field of dynamical chaos..

Динамическая система называется хаотической или нерегулярной, если она не удовлетворяет традиционным видам поведения, таким как монотонная или периодическая сходимость или расходимость, центральный или ограниченный цикл, ее временные серии выглядят случайными, как если бы это была стохастическая модель, хотя система полностью определенная и в ней не присутствует никаких случайных факторов [1].

Рассмотрим метрическое пространство (X,d). Будем называть отображение f: X®X хаотическим, если выполняются следующие условия:

1. f обладает существенной зависимостью от начальных условий.

2. f транзитивно.

3. Периодические точки f плотны в X

Строгая формулировка первого условия такова. Пусть x Î X, a U – открытое множество, содержащее x. Отображение f обладает существенной зависимостью от начальных условий, если для некоторого d существуют такое целое число n>0 и такая точка y Î U, что d(f⁽ⁿ⁾(x), f⁽ⁿ⁾(y))> d (здесь имеется в виду, f⁽¹⁾(x)=f(x), f⁽²⁾(x)=f(f(x)) и т.д.).

Отображение f называется транзитивным, если для любой пары U, V открытых множеств существует такое n ³ 0, что f⁽ⁿ⁾(U) Ç V не пусто.

Свойство плотности периодических точек означает, что в любой окрестности любой точки в X существует по крайней мере одна периодическая точка (и, следовательно, бесконечно много периодических точек) [5].

Хаотические динамические системы имеют замечательное свойство: они весьма податливы и чрезвычайно чувствительны к внешним воздействиям. Более того, динамикой хаотических систем можно управлять, то есть посредством слабых воздействий переводить такие системы из режима хаотических колебаний на требуемый динамический режим (тем самым, стабилизируя их поведение). Существует два основных способа стабилизации: без обратной связи и с обратной связью. Первый способ называется подавлением хаоса, второй - контролированием хаоса.

Методы хаотической динамики дают возможность при относительно малых энергетических затратах создать устройства принципиально нового типа, способные запоминать, шифровать и обрабатывать заданную информацию. Один из подходов к этому основан на том, что хаотические аттракторы (“притягивающие траектории”) содержат, как правило, бесконечное множество неустойчивых циклов. Для ряда систем разработаны методы, позволяющие либо стабилизировать эти циклы, либо создавать новые. Это является ключом к решению проблемы обработки информации и организации динамической памяти на основе использования систем с подавленным хаосом.

Рассмотрим динамическую систему с хаотическим аттрактором. В такой системе предельные циклы будут неустойчивыми. Каждому элементу алфавита поставим в соответствие один из циклов. В типичном хаотическом аттракторе имеется неограниченное число неустойчивых циклов. Значит, в принципе (без учета шума) таким способом может быть закодировано неограниченное число слов, причем записанная информация будет скрыта, ибо неустойчивые циклы практически ненаблюдаемы. Однако систему можно возмутить так, что нужный нам цикл станет устойчивым. Это позволяет извлечь закодированную информацию.

Опишем одну из реализаций этой идеи. Возьмем какую-либо динамическую систему с хаотическим аттрактором. Поставим в соответствие каждому стабилизированному (с помощью некоторого возмущения) циклу определенный символ алфавита. Вместо символа мы передаем на приемник стабилизирующее возмущение. Приняв возмущение, приемник применяет его к "зашитой" в нем той же самой динамической системе, и "смотрит", какой цикл при этом возник. А возникнет, разумеется, тот самый цикл, который обозначен переданным символом.

Но какая разница - передать сам символ или возмущение, стабилизирующее соответствующий ему цикл? Во-первых, для многих хаотических систем можно разработать эффективный сценарий поиска возмущений, приводящих к стабилизации цикла, проходящего через заданные точки. Эти точки можно выбрать случайным образом - тогда и стабилизирующее возмущение будет выглядеть как случайная последовательность параметров. Во-вторых, в ряде систем одному и тому же циклу (то есть символу) соответствует не одно, а целая область стабилизирующих возмущений. При каждой передаче этого символа можно выбирать параметры из этой области тоже случайным образом! Поэтому в передаваемой последовательности не будет повторений, связанных с кодированием идентичных символов алфавита, и отличить этот сигнал от шума будет невозможно; к тому же "противнику" для расшифровки необходимо знать конкретный вид динамической системы, который в данном случае является ключом [3].

Предлагаемый метод был реализован на компьютере на основе квадратичной дискретной динамической системы, действие которой состоит в итеративном применении отображения

X_t+1 = a X_t (1 - X_t )

(параметр a принадлежит интервалу (0,4]). Он позволил создать экспериментальную систему шифрования символов, вводимых с клавиатуры персонального компьютера. Кратко опишем эту систему.

При использовании компьютера типа IBM PC каждый символ, вводимый с клавиатуры, кодируется целым числом (ASCII-кодом), принадлежащим отрезку [0,255]. Каждому символу можно поставить в соответствие последовательность из трех целых чисел - десятичных цифр ASCII-кода n₁, n₂, n₃. Например, символу A с ASCII-кодом 65 отвечает тройка чисел n₁ = 0, n₂ = 6, n₃ = 5. Каждому из этих трех чисел ставится в соответствие последовательность параметров a, стабилизирующая цикл периода n_i + 2. Полученная в результате такого кодирования последовательность транслируется на приемник, в котором находится дешифратор. На дешифраторе последовательность параметров преобразуется в последовательность целых чисел, соответствующих периодам циклов. Из каждого полученного целого числа необходимо вычесть 2. Теперь, сгруппировав эти числа по три, легко получить ASCII-код символа и, таким образом, сам символ.

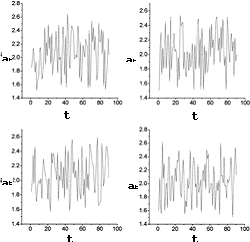
Рис.1.

Результаты работы кодирующей программы представлены на рис. 1. и 2. На рис. 1 изображены четыре различных варианта кодирующих последовательностей параметров для слова CHAOS. На рис. 2 графически представлена последовательность параметров, кодирующая строку из десяти одинаковых символов "c" [2].

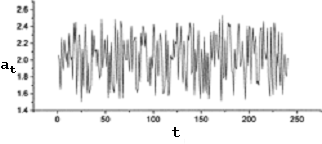
Рис.2.

Таким образом, в данной системе ключом будет, во-первых, вид самой функции (а она может быть определена на каком-либо пространстве функций), во-вторых, конкретные параметры, входящие в эту функцию, в-третьих, система представления символов «исходного» текста значениями параметров. Так как установлению цикла длины n соответствует не одно значение параметра, а целая область параметров, то при выборе значения из этой области случайным образом и искажении несложным преобразованием, при передаче даже одного и того же символа мы получим поток, неотличимый от «шума» (см. Рис.2).

Изложенные выше идеи позволяют разработать математическую и информационную модель использования криптографического алгоритма на основе теории хаоса для передачи информации в телекоммуникационных системах с высокими требованиями к конфиденциальности передаваемой информации, таких, например, как банковские информационные системы.

Литература

1. Pierre N.V.Tu. Dynamical Systems. An Introduction with Applications in Economics and Biology. Springer-Verlag, Berlin - Heidelberg, 1994.

2. Дмитриев А. С., Старков С. О. Передача сообщений с использованием хаоса и классическая теория информации. Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 1998.

3. Лоскутов А. Ю., Михайлов А. С. Введение в синергетику. - М.: "Наука", 1990.

4. А.П. Алферов, А.Ю. Зубов, А.С.Кузьмин, А.В. Черемушкин. Основы криптографии. Москва, «Гелиос АРВ», 2001

5. Ричард М. Кроновер. Фракталы и хаос в динамических системах. Москва «Постмаркет», 2000.