КОНСТРУИРОВАНИЕ МЕТОДОВ ВЫБОРА И РАНЖИРОВАНИЯ НА ОСНОВЕ ФУНКЦИОНАЛЬНОГО БАЗИСА

Начальная версия системы выбора и ранжирования СВИРЬ [1] имела целью реализацию всех «классических» методов рационального выбора объектов из заданного дискретного множества. В основу системы была положена классификация известных методов выбора, предложенная в работе [2]. Однако, как показала практика, перечень методов оказался открытым. На следующем этапе разработки в систему были включены в качестве самостоятельных методы мягких притязаний и балльной оценки [3]. По отношению к взятой за основу классификации они оказались комбинированными методами. На этом потребность в комбинировании методов не закончилась. Практика выдвигала всё новые требования к методам рационального выбора, реализовать которые в рамках «методоориентированной» технологии проектирования системы не представлялось возможным.

Для обеспечения универсальности системы и возможности её дальнейшего развития была принята парадигма «функционального» проектирования системы. Её идея заключается в построении такого функционального базиса, который позволял бы конструировать любой из методов выбора объектов в дискретном множестве. Естественным «ограничителем» совокупности методов выбора явился перечень задач, решаемых системой. Они были разделены на 3 класса: отбор, упорядочение и классификация объектов.

В докладе рассматриваются задачи, решаемые новой версией системы выбора и ранжирования объектов СВИРЬ и функции, используемые для синтеза методов выбора.

1. Отбор объектов

Задачи отбора объектов в системе отнесены к более общему классу задач классификации. Последние различаются как решающими правилами, с помощью которых объекты разделяются на классы, так и интерпретацией самих классов. Тогда как обычная классификация предполагает равноценность классов, в теории принятия решений объекты, разделяемые на 2 класса, принято делить на допустимые и недопустимые. По отношению к недопустимым объектам процесс разделения на 2 класса называется отсеиванием, а по отношению к допустимым объектам – селекцией или отбором. Таким образом, задачи отбора характеризуются прагматическим подходом – из исходного множества объектов X отбираются только полезные или допустимые. Отсеиваемые объекты, отнесённые к бесполезным, исключаются из рассмотрения.

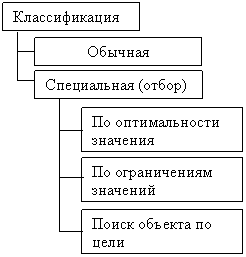
Полезность объектов оценивается в пространстве характеризующих их признаков. Отсюда задачи отбора различаются видом требований, предъявляемых к этим признакам (см. рис.1).

Рис.1. Классификация задач отбора в пространстве признаков

Результатом отбора объектов из исходного множества X является некоторое его подмножество X_s, обладающее требуемыми свойствами. Объекты, отбираемые относительно оптимальности значений характеризующих их признаков, образуют множество недоминируемых альтернатив (множество Парето). Объекты, отбираемые относительно ограничений, накладываемых на значения характеризующих их признаков, образуют множество допустимых альтернатив. Поскольку эти ограничения принято называть также уровнями притязаний, метод выделения объектов, удовлетворяющих этим уровням, называют методом притязаний [2]. Поиск объекта по цели представляет собой частный случай метода притязаний, когда известны точные значения признаков, которым должен удовлетворять объект.

2. Упорядочение объектов

Решение задач этого класса основано на измерении объектов в порядковой шкале, так как целью упорядочения является присвоение каждому объекту места среди остальных. Поскольку этому требованию не удовлетворяет векторное представление объектов, для решения задачи упорядочения объектов по их признакам необходимо либо упорядочить сами признаки относительно их важности (значимости), либо сопоставить каждому вектору скаляр, учитывающий соотношение значимости признаков.

1-й подход реализуется методом приоритетов, который осуществляется поиском объектов с оптимальными значениями критериев в направлении убывания значимости критериев. Поскольку нахождение оптимума гарантировано только для наиважнейшего критерия, значения остальных критериев для наилучшего объекта являются условно-оптимальными.

Для отображения вектора в скаляр используется функция свёртки исходных критериев: f:Y´…´Y®Y, вид которой является предметом соглашения между заинтересованными лицами. Функция свёртки f названа в [2] суперкритерием, что характеризует две её особенности: объединяющий и надкритериальный характер по отношению к исходным критериям. В силу произвольного характера функции свёртки суперкритерий не обеспечивает однозначности решения задачи упорядочения. Поэтому выбор функции свёртки f является важным этапом решения задачи упорядочения. В соответствии с используемым принципом задачи этой группы относятся к задачам скалярной оптимизации.

Упорядочение объектов может выполняться не только относительно значений характеризующих их признаков, но и относительно требований, предъявляемых к этим значениям. В этом случае упорядочению подлежит степень отклонения значений признаков от предъявленных к ним требований.

Упорядочению могут подлежать не только все объекты из множества X, но и их часть, предварительно отобранная в множество X_s. При этом на метод упорядочения оказывает влияние использованный для получения X_s метод отбора. На рис.2 приведена классификация задач упорядочения объектов в n-мерном пространстве признаков.

Рис.2. Классификация задач упорядочения

Согласно изложенному выше, в качестве классифицирующих выбраны следующие признаки:

· Использование предварительного отбора объектов;

· Исходные данные для упорядочения;

· Способ упорядочения.

Задачи нижней ветви классификации являются комбинированными, поскольку совмещают задачи отбора и упорядочения объектов.

1. Функциональный базис задач выбора

Функциональный базис F многокритериального оценивания объектов делится на 2 части: F=F_МÈF_П. Первая часть F_М служит для конструирования метода выбора, а вторая F_П – для настройки каждого оцениваемого признака.

В множество F_М включены функции, используемые для решения всех 3-х классов задач: отбора, упорядочения и классификации объектов.

Функция f₁ задаёт вид решаемой задачи. Если это – задача отбора объектов, то функция f_О1 задаёт общие требования к признакам (оптимальность, интервал или точное значение), а функция f_О2 определяет необходимость оценки отобранных объектов на предмет их упорядочения.

Задача упорядочения (ранжирования) объектов требует большего числа функций. Функция f_Р1 фиксирует необходимость предварительного отбора. Если он необходим, то для его выполнения задаётся функция f_О1. Для выполнения упорядочения объектов с помощью функции f_Р2 задаётся общее требование к признакам (соответствие заданным значениям или преимущество по значениям).

С помощью функций f_Р3 и f_Р4 задаются шкалы значений функции полезности (общая оценка) и значимости критериев оценки. Функция полезности использует 3 шкалы: нормированную [0,1], ненормированную [0,Z], балльную [1,N], где Z и N – действительные числа. Нормированная шкала применяется в случае разнородных, а ненормированная шкала – в случае однородных признаков. Балльная шкала используется для пересчёта оценок, полученных в нормированной шкале, в баллы с целью получения балльной оценки. Границы балльной шкалы задаются функций f_Р5. Для задания значимости критериев оценки используется порядковая, либо интервальная шкала.

Функция f_Р6 служит для задания функции полезности. Помимо стандартных аддитивной и мультипликативной свёртки критериев функция полезности может иметь произвольную форму. Для случая однородных массивов, используемых в теории игр (матрицы выигрышей и платежей), функция полезности реализует максиминную и минимаксную стратегии.

Точность значения функции полезности может регулироваться функцией f_Р7.

Использование функций из множества F_П зависит от функции-ключа f_П1, задающей участие рассматриваемого признака в оценивании объектов. Использование остальных функций из множества F_П определяется выбранным методом оценивания объектов. При оптимизации критериев используется функция задания направления оптимизации f_П2. Диапазон

изменения признака устанавливается либо его граничными значениями в совокупности объектов (функция f_П3), либо задаётся пользователем (функция f_П4). С помощью функции f_П5 задаётся тип ограничений при решении задачи отбора объектов.

Как следует из изложенного, стремление к максимальной независимости функций не привело к полному достижению этой цели. Однако, это не следует считать недостатком системы, поскольку чётко определились границы комбинирования функций для реализации различных методов оценивания объектов.

4. Технология решения задач выбора

Решению задачи выбора на системе СВИРЬ предшествуют следующие подготовительные этапы: структурирование признаков, характеризующих оцениваемые объекты, определение значений признаков, формирование критериев, подлежащих оцениванию, задание условий выбора. В отличие от методоориентированной версии системы СВИРЬ, в которой задание условий выбора основано на задании используемого метода, в новой версии системы требуемый метод выбора синтезируется как набор составляющих его функций, начиная с выбора решаемой задачи и кончая выбором шкал, используемых для представления значений исходных данных и результатов.

На рис.3 приведено окно задания условий выбора, настроенное на реализацию метода упорядочения объектов. В левой половине панели выполняется настройка функций, характеризующих используемый метод оценивания, а в правой половине задаются требования к участвующим в оценивании объектов признакам. Каждый признак настраивается индивидуально.

Изложенный в докладе принцип конструирования методов выбора обладает высокой степенью универсальности.

Литература

1. Микони С.В., Козченко Р.В., Созоновский П.Г. Выбор наилучших вариантов из баз данных// Сборник докладов Международной конф. по мягким вычислениям и измерениям SCM’1999. –СПб.: СПбГЭТУ, 1999

2. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. –М.: Высшая школа, 1989.

3. Микони С.В. Методы мягкого выбора//Труды конф. КИИ-2000, -М.: Изд-физ.мат.лит-ры, 2000, том 2, с.472–479.

КОНСТРУИРОВАНИЕ МЕТОДОВ ВЫБОРА И РАНЖИРОВАНИЯ

С.В.Микони, М.И.Сорокина