Введение
Использование наглядности в представлении
сложной системы с одной стороны повышает ее информативность, а с другой - позволяет находить новые закономерности и
законы ее функционирования. Гильберт [1] отмечал: «В
математике, как и вообще в научных исследованиях, встречаются две тенденции:
тенденция к абстракции - она пытается выработать логическую точку зрения на
основе различного материала и привести весь этот материал в систематическую
связь, и другая тенденция, тенденция к наглядности, которая в противоположность
этому стремится к живому пониманию объектов и их внутренних отношений».
Трудно выделить какие-то общие критерии,
которые характеризуют термин «наглядность», скорее всего «существует категориальная
интуиция, которая непосредственно дает общие отношения между объектами. Такими
общими отношениями являются расположенность объектов, отношение части и целого,
принадлежности признака предмету, категории действия и т.п.» [2].
Примеры наглядного представления множества
структур сложной системы
Будем исходить из того, что существует «принцип
(закон) 100% эффективности математики, суть которого состоит из двух утверждений
- прямого и обратного. Для любой реальности (явления, процесса
и т.д.) и любой наперед заданной (но не абсолютной) точности существует
математическая структура, которая описывает эту реальность с заданной
точностью, и, обратно, для любой математической структуры и любой точности
существует реальность, которая описывается этой структурой с этой точностью»
[5].
Под
анализом структуры сложной системы в рамках данной статьи будем понимать анализ
законов ее изменения и характеристик элементов в процессе эволюции. С этой
целью определим шаги задания множества структур системы:
1) определяется минимальная конфигурация системы и правило построения произвольной структуры системы. Это следует из определенного в [8] правила формального синтеза;
2) на множестве полученных структур определяется отношение упорядоченности и строится решетка структур;
3) каждый элемент решетки структур имеет свой структурный номер и каждому элементу ставятся в соответствие некоторые значения, которые являются оптимизационными или анализируемыми параметрами;
4) в зависимости от заданных условий определяются элементы решетки структур, удовлетворяющие заданным критериям.
Преимущество
такого подхода состоит в том, что благодаря предварительному упорядочиванию
множества структур, значительно упрощается поиск структур,
удовлетворяющих заданным критериям. В какой-то степени это
можно сравнить с индексированными базами данных, в которых поиск требуемой
записи осуществляется значительно быстрее, чем в неиндексированной. Диаграммы Хассе для упорядоченного
множества отражают только их основное свойство - частичную упорядоченность.
Другие важные свойства, которыми они обладают, выпадают из визуального рассмотрения.
Более того, отсутствие некоторого алгоритма построения может привести к тому,
что зрительное построение образа, основанное только на отношении упорядоченности
или на регулярности вершин, станет вычислительно сложной задачей.
Рассмотрим дистрибутивные решетки и определим
для них правила построения:
1) количество элементов в структурном
номере определяет пространственную размерность решетки, которая будет проецироваться
на плоскость. Построение начинается с минимального элемента;
2) множество уровня располагается на одной
прямой. Увеличение размерности решетки увеличивает размерность пространства;
3) каждая координатная ось однозначно
определяет правило увеличения структурного номера элемента;
5)
проекция
решетки на плоскость выбирается таким образом, чтобы никакие две вершины не
оказались наложенными друг на друга;
6)
обозначения вершин пишется рядом с вершиной,
характеристика вершины пишется внутри вершины.
Наглядные методы построения структуры сложных
систем
Рассмотрим структуру произвольной
платежной системы, которую по количеству элементов, связей между ними,
иерархичности можно отнести к сложной системе. Из анализа
таких структур следует, что базовыми элементами являются процессинговые
центры, точки обслуживания и банки-эмитенты. Закон функционирования платежной
системы кратко можно описать следующим образом: процессинговые
центры собирают финансовые транзакции от точек обслуживания и рассылают
обработанные транзакции эмитентам и эквайрерам. В общем
случае структура платежной системы может быть многоуровневой, в которой могут
быть главные, региональные и т.д. процессинговые
центры.
Определим
упорядоченное множество таких структур. Будем считать, что система является
двухуровневой. Минимальными элементами структуры системы s(p,Q)
являются главный процессинговый центр, региональный процессинговый центр, банк-эмитент и точка обслуживания,
подключенные к региональному процессинговому центру.
Здесь p -
количество региональных процессинговых центров, а Q =(q1,q2....qi....qp)
- упорядоченное множество количеств банков-эмитентов, подключенных к каждому
региональному процессинговому центру. Здесь (q1 £
q2 £....qi £...£ qp).
Таким образом, минимальную структуру платежной системы можно записать как s(1,2). Поскольку реальная система не может
быть наращена до бесконечности, введем значение max(p),
означающее максимальное количество региональных процессинговых
центров, и значение max(q), означающее максимальное количество
эмитентов и точек обслуживания, подключенных к одному региональному процессинговому центру. Для того чтобы задать рекурсивное
правило построения произвольной структуры платежной системы, дополнительно введем
служебный параметр i,
который определяет текущий номер банка-эмитента. Тогда s(p,Q)=s(p,Q,i).
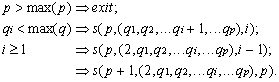
Указанное выше рекурсивное определение задает множество структур S={sj}. На данном множестве S введем отношение “³”, которое означает, что две произвольные структуры платежной системы sj и sk находятся в этом отношении тогда и только тогда, когда количество региональных процессинговых центров в первой структуре больше или равно количеству региональных процессинговых центров во второй структуре, а количество банков-эмитентов и точек обслуживания у региональных процессинговых центров первой структуры больше или равно количеству банков-эмитентов и точек обслуживания у соответствующих региональных процессинговых центров второй структуры. Формально это выглядит как
![]() .
.
Указанное отношение обладает свойством рефлексивности, транзитивности и антисимметричности, следовательно, S=(S,³) - частично упорядоченное множество (ЧУМ). На заданном ЧУМ S для любых двух sj и sk введем понятие точной верхней и нижней граней sup(sj , sk ) и inf(sj , sk ).
![]()
Можно показать, что минимальные нижние и верхние грани существуют для любых двух элементов ЧУМ S, следовательно, S – решетка. Диаграмму решетки построим в соответствии с определенными ранее правилами построения на основе отношения упорядоченности. В результате получим изображенное на рис.1 упорядоченное множество всех структур системы.
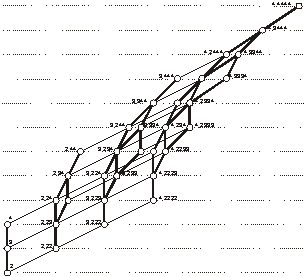
Рис. 1
Разумеется, это не единственный пример. На
основе анализа структур систем распознавания, определения минимальных элементов
системы, выбора отношения упорядоченности, используя правила построения, можно
построить решетку структур систем распознавания, изображенную на рис.2
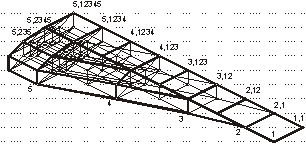
Рис.2
Наглядные методы анализа элементов сложных
систем
Рассмотрим формат транзакции (протокол обмена) между элементами системы. В
зависимости от условий работы, роста, жизненного цикла системы он может как сдерживать, так и способствовать ее развитию. Для
анализа формата воспользуемся решеткой разбиений D, отношение упорядоченности элементов
которой определено в [4]. Возьмем 10-ти элементное множество и построим решетку
D10, используя предложенное правило
построения. В результате получим решетку, изображенную на рис. 3. Нижний
элемент решетки обозначается (1111111111), крайний правый – (22222).
Если система развивается, то количество
параметров и множество их значений, как правило, также требует увеличения. Однако
это не всегда просто осуществить. Для принятия решения назначим каждому элементу
решетки количество номеров, которое можно получить при данном разбиении, и
отметим дуги, соединяющие вершины с одинаковым количеством номеров жирными
линиями, разбив все множество таким образом на классы
эквивалентности. Сразу же можно провести наглядную оценку, что классами
эквивалентности являются пути, максимально приближенные к пути из элемента
(1111111111) в элемент (22222).
Указанная решетка тесным образом связана с
числами Стирлинга 2-го рода. Например, 511 означает число способов разбиения
10-ти элементного множества на два непустых подмножества, а для каждой из пяти
вершин, находящихся на этом уровне можно указать число способов для каждой из
возможных пар разбиений (10 + 45 + 120 + 210 + 126).
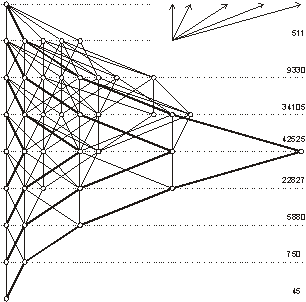
Рис.3
Интересно, что в такой постановке для
чисел имеются явные зрительные образы. Решетка на рис. 3 является зрительным образом
числа 115975 как числа всех разбиений 10-ти элементного множества. Это соответствует
пифагорийскому тезису «все вещи суть числа» [7]. То-же самое характеризуют слова Н.
Винера: «Едва ли кто нибудь из математиков в состоянии освоиться с мыслью, что
цифры могут представлять собой культурную или эстетическую ценность… Я
решительно протестую против этого косного представления о математике».
Анализ жизненного цикла системы
Пусть для множества структур некоторой
системы мы построили решетку, в соответствии с которой в процессе эволюции
структура системы может развиваться от некоторого начального элемента до максимального. Если не происходит краха системы, она
постепенно будет деградировать. Процесс деградации, например, может происходить
по одному из возможных путей из 0 в 1 на решетке, показанной на
рис. 4. Эта решетка симметричная. Нижняя часть определяет процесс роста,
верхняя – процесс упадка (деградации) системы.
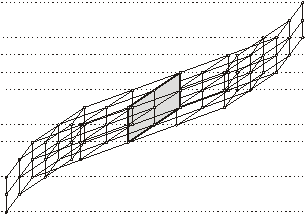
Рис. 4
Заключение
В работе [3] говорится об эстетической привлекательности фрактальных объектов,
поскольку возможно аналогичные динамические структуры возникают в сознании человека.
Мне кажется, эстетика алгебраических структур также привлекательна, но это уже
дело вкуса.
Литература
1.
Гильберт Д., Кон-Фоссен С. Наглядная Геометрия:
Пер с нем. - 3-е изд. - М: Наука, 1981. - 344 с.
2.
Горохов В.Л. Основные конструктивные философские посылки отображения
многомерных данных в когнитивные образы. Труды Международной конференции по мягким
вычислениям и измерениям. 25-27 июня 2002 г. Санкт-Петербург SCM-2002.
3.
Горохов В.Л. Механизмы восприятия когнитивных образов, технические пути
их активизации. Труды Международной конференции по мягким вычислениям и измерениям.
25-27 июня 2002 г. Санкт-Петербург SCM-2002.
4.
Айгнер. Комбинаторная теория. Пер. с англ. -
М.: Мир, 1982. - 558 с.
5.
Бутковский А.Г. Философия, методология и математика единой
геометрической теории управления. //Проблемы управления и моделирования в
сложных системах: Труды IV международной конференции,
Самара, Самарский научный центр РАН 2002, с 4.
6.
Грэхем Р., Кнут Д., Поташник О. Конкретная математика. Пер. с англ. -
М.: Мир, 1998. - 703 с.
7.
Волошинов А.В.
Математика и искусство. 2 изд. дораб. и доп. - М.: Просвещение, 2000. – 399 с.
8. Смальянц Р. Теория формальных систем. Пер. с англ. - М.: Наука, 198