Динамика электромехатронных устройств может быть описана системой уравнений Лагранжа - Максвелла:
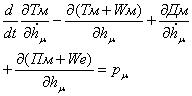 ,
,
![]() , (1)
, (1)
где Тм – кинетическая
энергия системы, Пм потенциальная энергия, Дм и Де –
мощности рассеяния энергии в механической и электрической частях системы, Wм –
магнитная энергия системы, Wе – электрическая энергия, а hμ и
h’μ – механические координаты системы и их производные по
времени, qv и q’v – электрические координаты и их
производные по времени (заряды и токи в контурах).
Эти уравнения получены из
уравнений Лагранжа, применяемых для описания динамики механических систем,
путём применения электромеханических аналогий [Л1-3], согласно которым
магнитная энергия Wм аналогична кинетической энергии
Тм, а электрическая энергия Wе - потенциальной Пм.
Приведённые выше уравнения
Лагранжа-Максвелла можно разделить на две группы: уравнения, описывающие динамику механической части
системы и уравнения, описывающие процессы в электрических контурах системы.
Причём каждое из электрических уравнений соответствует закону Кирхгофа для
отдельного независимого контура.
Пользуясь
электромеханическими аналогиями, можно представить каждое из механических
уравнений как уравнение некоторой электрической замкнутой цепи (контура), в
котором обобщённая координата hμ – соответствует заряду, а
производная от координаты (обобщённая скорость) h’μ – току.
Тогда от уравнений Лагранжа
– Максвелла можно перейти к эквивалентным схемам электромеханических (механических)
цепей, содержащих количество независимых контуров, равное числу уравнений.
Такой подход позволяет комплексно представить динамику электромеханической
системы и применять для исследования динамики механической части системы методы
и пакеты прикладных программ, используемые, для анализа электрических цепей
(например - DesignLab, Micro-Cap и др.).
Данный подход был применён
при исследовании динамики манипулятора с гибкой связью.
Объект управления
представляет собой перевёрнутый маятник с гибкой связью между валом двигателя и
исполнительным органом, схематически представленный на рис. 1. Объект также
можно представить как гибкую руку, угол между звеньями которой зависит от
гибкости пружины и динамики движения. Задачей управления является достижение
конечной точки второго звена заданной скорости φ‘k и на
заданном угле φk для осуществления броска предмета с помощью
поворота первого звена во времени на некоторый угол φ1(t).
В данном случае в качестве
исполнительного двигателя рассматривается двигатель постоянного тока,
обладающий собственной динамикой связанной с электрической и механической
инерционностью его якоря. Поскольку ДПТ является скоростным двигателем,
управляемым с помощью якорного напряжения Uдв,
то он приводит во вращение исполнительный орган манипулятора через понижающий
редуктор с коэффициентом передачи n.
Динамика рассматриваемой
электромеханической системы описывается следующими уравнениями [Л4]:
![]() ; (2)
; (2)
![]()
(3)
![]() ; (4)
; (4)
![]() ,
,
![]() , (5)
, (5)
где ρ – коэффициент
трения, σ – коэффициент жёсткости пружины, I1 – момент инерции двигателя,
М – электродинамический момент двигателя, Ея – противо - э.д.с. якорной цепи, Кэм
– электромагнитный коэффициент двигателя, Lя
и Rя
– соответственно индутивность и сопротивление цепи якоря двигателля, Iя – ток якоря.
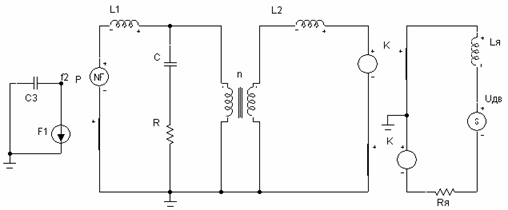
По этим уравнениям может
быть построена электромеханическая модель системы, в которой обобщённые силы
представлены в виде эквивалентных э.д.с, а скорости в
виде токов. Схема модели представлена в виде электрической цепи на рис. 2. Она
содержит три контура, соответствующих уравнениям (2)-(4). Контур 1 – является
контуром якорной цепи ДПТ. И соответствует уравнению (4); контур 2 – является эквивалентной
схемой механической части двигателя соответствует уравнению (3), а контур 3
является эквивалентной схемой исполнительного органа манипулятора, что
соответствует уравнению (2), где Р – обобщённая сила
тяжести (Р=m*l*g*sin(φ2)). Контура
1 и связаны прямой и обратной связью через источник напряжения управляемый
током (ИНУТ). ИНУТ1 отображает прямое
воздействие двигателя на исполнительный механизм, а ИНУТ2 – обратную реакцию
механизма на двигатель.
Одним из достоинств представления электромеханической системы в виде многоконтурной
электрической цепи, полученной на основе электромеханических аналогий, является
на наш взгляд её «физичность». Компьютерное моделирование системы в таком виде
с применением, например, пакета MicroCap, даёт возможность получить
полную картину токов э.д.с., скоростей и моментов, возникающих в различных
частях системы, и таким образом выявить существенные факторы, влияющие на динамику
системы, и в ряде случаев отбросить несущественные.
Другим достоинством такого
представления является ненаправленность элементов эквивалентной схемы, что даёт
возможность обращать отдельные части схемы с целью синтеза управлений,
необходимых для получения заданных движений, то есть решать обратную задачу динамики.
В частности для
рассматриваемой «гибкой руки» одним из оптимальных режимов является режим «управляемого
резонанса» [Л5], когда в течении половины периода
собственной частоты колебаний происходит разгон с постоянным ускорением, а
затем в течение четверти периода – движение с постоянной скоростью [Л6].
Может быть поставлена задача
программно – логического управления ДПТ для получения такого режима движения
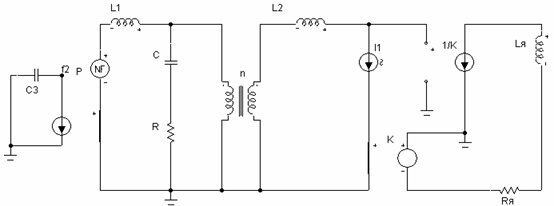
исполнительного механизма манипулятора. Для решения этой
задачи удобно представить эквивалентную электрическою схему «руки» с обратной
моделью ДПТ, как показано на рис. 3. Здесь в контуре 2 источник обобщённой
э.д.с. М заменён источником тока ω, генерирующим скорость ω заданной
формы, а возникающий при этом момент М через ИТУН1
генерирует нужный ток двигателя Iя. Наблюдая возникающее при
этом напряжение Uдв, можно, аппроксимировав
его, получить необходимое воздействие на двигатель для получени заданного
разгона механизма.
Проводимые в лаборатории
электромеханики и электромехатроники кафедры АиВТ СПбГТУ исследования
мехатронных устройств методами электромеханических аналогий с применением
пакетов DesignLab и MicroCap показали удобство такого подхода для моделирования электромеханических
устройств, исследования их динамики и оптимизации их параметров.