Задача структурно-параметрической идентификации относится к классу обратных задач кибернетики, а поэтому относится к некорректно-поставленным задачам. При решении этой задачи можно рассматривать различные виды неопределенностей [1]: незнание структуры математической модели динамического объекта, неточность определения значений параметров модели, неточность измерений вход-выходных переменных объекта, обусловленная метрологическими характеристиками измерительной аппаратуры, и т. п.
Существующие подходы, в которых исходными данными являются измеренные со случайной ошибкой в равноотстоящие моменты времени значения вход-выходных переменных объекта, реализуют отношение толерантности между эмпирической и математической моделями объекта. Как отмечается в [2], отсутствие свойства транзитивности между моделями является принципиальным препятствием в построении цепочки отношений, строго соединяющих два объекта.
В работе предлагается подход решения указанной задачи, реализующий принцип эквивалентности между моделями. Начальные исследования проводились в детерминированной постановке и были связаны с неопределенностями структуры и значений параметров.
Сущность подхода в сжатой форме можно представить следующими взаимосвязанными теоретическими положениями, сформулированными для динамических систем, допускающих линеаризацию. Математические модели таких систем рассматривались в форме передаточных функций и в форме интегралов Дюамеля. Для реализации отношения эквивалентности непрерывной и дискретной моделей в качестве критерия идентификации рассматривалось равномерное приближение, т. е. равенство входных воздействий в дискретные моменты времени влечет равенство реакций систем.
Первое положение связано с установлением и исследованием свойств взаимнооднозначного соответствия между непрерывными и дискретными моделями, основанного на согласованном Z-преобразовании z=esDt. Для этого преобразования в качестве однолистных областей выступают бесконечное множество полос шириной 2p/Dt, где Dt – период дискретизации. Для осуществления взаимнооднозначного отображения приходим к построению римановой поверхности, включающей бесконечное число z-плоскостей, соединенных между собой вдоль кривых, получивших название «разрезы». Исследован механизм изменения взаимнооднозначного соответствия при изменении периода дискретизации Dt. В качестве основного результата сформулирован принцип вариации периода дискретизации: взаимнооднозначное соответствие между моделями имеет место тогда и только тогда, когда при изменении Dt все полюса и нули непрерывной передаточной функции покрываются нулевой полосой (-p/Dt, p/Dt). Заметим, что в z-плоскости нули и полюса дискретной передаточной функции перемещаются вдоль определенных траекторий и при уменьшении Dt стремятся к точке (1, 0). Таким образом, указанное исследование позволяет ввести отношение эквивалентности моделей на некотором множестве значений Dt Î (Dtmin, Dtmax).
Второе положение связано с разработкой точного восстановления дискретной передаточной функции по дискретным измерениям вход-выходных переменных.
В качестве основы такого способа были использованы свойства и алгоритмы непрерывных дробей [3]. Такой алгоритм реализован в форме метода В. Висковатова и его модификации. Построение модели осуществляется с помощью итерационного алгоритма формирования иденти-фицирующей матрицы, в которой первые две строки состоят из временных последовательностей дискретных измерений вход-выходных переменных объекта. Критерием останова в данном случае является появление нулевой строки, тогда нулевой столбец матрицы восстанавливает дискретную передаточную функцию, а если ввести оператор сдвига по времени, то и дискретную модель. Такой подход получил название способа SP-идентификации.
Модельные и практические исследования показали широкие возможности способа SP-идентификации как в части динамических свойств систем (высокий порядок, устойчивость и неустойчивость, неминимально-фазовость, колебательность и т. д.), так и в части разновидностей систем (системы с переменным запаздыванием, системы со статической нелинейностью типа реле, люфта, и т.д.).
В работе осуществляется обобщение метода SP-идентификации на случай неточности измеренных значений вход-выходных переменных динамической системы. Согласно [1], этот случай приводит к исходным данным, заданным интервально.
Предлагаемый интервальный моди-фицированный метод Висковатова основан на использовании интервальной математики [4] и аппарата непрерывных дробей [3] и позволяет на основе дискретных измерений значений вход-выходных переменных получить интервальную дискретную передаточную функции, а также модель в форме конечно-разностного уравнения с интервально-значными коэффициентами.
Рассмотрим линеаризованный динамический объект с непрерывным входным воздействием x(t), непрерывным выходным воздействием y(t), непрерывной передаточной функцией G(s).
Необходимо на основе измеренных дискретных значений вход-выходных переменных построить интервальную дискретную модель передаточной функции объекта.
Произведем дискретизацию вход-выходных величин с заданным периодом Dt, в результате получаем последовательности отсчетов x(nDt) и y(nDt), n = 0, 1, … . Для построения исходных интервалов
[x(nDt)-ex, x(nDt)+ex] и [y(nDt)-ey, y(nDt)+ey], n = 0, 1, 2, …. используются наибольшие значения ex > 0 и ey > 0 погрешностей средств измерений, называемые пределами допускаемых погрешностей средств измерений и устанавливаемые нормативно-техническим документом для данного типа средств измерений.
Далее строим идентифицирующую матрицу с интервальными элементами
[amn, bmn],
где a0n =
x(nDt)-ex, b0n = x(nDt)+ex,
a1n = y(nDt) - ey, b1n = y(nDt) + ey, n = 0, 1, …, а границы следующих элементов матрицы вычисляются последовательно:
![]() .
.
Правила интервальной арифметики позволяют преобразовать это выражение к следующему виду:
amn = min(max(am-2,n+1/am-2,0; am-2,n+1/bm-2,0;
bm-2,n+1/am-2,0;
bm-2,n+1/bm-2,0)–min(am-1,n+1/am-1,0;
am-1,n+1/bm-1,0; bm-1,n+1/am-1,0; bm-1,n+1/bm-2,0);
min(am-2,n+1/am-2,0; am-2,n+1/bm-2,0;
bm-2,n+1/am-2,0; bm-2,n+1/bm-2,0)–max(am-1,n+1/am-1,0;
am-1,n+1/bm-1,0; bm-1,n+1/am-1,0; bm-1,n+1/bm-2,0)),
bmn = max(max(am-2,n+1/am-2,0; am-2,n+1/bm-2,0;
bm-2,n+1/am-2,0;
bm-2,n+1/bm-2,0)–min(am-1,n+1/am-1,0;
am-1,n+1/bm-1,0; bm-1,n+1/am-1,0; bm-1,n+1/bm-2,0);
min(am-2,n+1/am-2,0; am-2,n+1/bm-2,0;
bm-2,n+1/am-2,0; bm-2,n+1/bm-2,0)–max(am-1,n+1/am-1,0;
am-1,n+1/bm-1,0; bm-1,n+1/am-1,0; bm-1,n+1/bm-2,0)),
m = 2, 3, 4, …, n = 0,
1, 2, …
Поскольку вычисление коэффициентов идентифицирующей матрицы связано с операцией интервального деления, то вычисление интервальных элементов матрицы прекращается с появлением строки, все элементы которой содержат в себе число 0. Появление «нулевой» строки однозначно определяет длину непрерывной дроби, то есть порядок дискретной модели.
Из элементов нулевого столбца идентифицирующей матрицы составляется правильная С-дробь с интервальными коэффициентами:
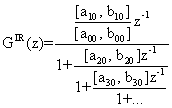 ,
,
где z – переменная согласованного Z-преобразования.
Пользуясь правилами интервальной арифметики, полученную непрерывную дробь преобразуем в дискретную передаточную функцию в виде дробно-рационального выражения с коэффициентами-интервалами:
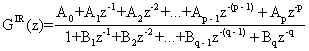 где
где ![]() ,
, ![]() .
.
Таким образом, получена интервальная модель объекта в виде дискретной передаточной функции объекта. Интервальные коэффициенты содержат в себе истинные значения коэффициентов.
Интерпретируя z-1 как оператор обратного временного сдвига, произведем переход во временную область, от интервальной дискретной передаточной функции к интервальной модели дискретной динамической характеристики объекта в виде конечно-разностного уравнения:
y(n)=A0x(n)+A1x(n-1)+…+Apx(n-p)-
-B1y(n-1)-B2y(n-2)-…-Bqy(n-q),
n=0,1,2,…, x(i)=x(iDt), y(i)=y(iDt), i=0,1,2,…,
![]() ,
, ![]() .
.
Полученную интервально-значную функцию можно представить двумя граничными вещественными функциями ymin(n) и ymax(n), образующими интервалы вида:
y(n) = [ymin(n),
ymax(n)] , n = 0, 1, 2, …
На рисунке приведена точная переходная характеристика объекта y(t), верхняя и нижняя граничные функции ymin(n) и ymax(n). Очевидно, что истинные значения характеристики лежат в интервалах, построенных интервальным модифицированным методом Висковатова.
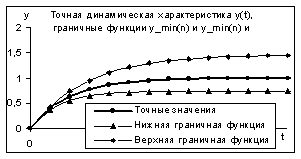
Степень неточности интервальной модели, то есть ширина получаемых интервалов, зависит от выбранного периода дискретизации Dt и от значений пределов допускаемых погрешностей средств измерения ex и ey. При уменьшении ex и ey точность интервальной модели естественным образом возрастает.
Рассмотрим пример применения интервального модифицированного метода Висковатова. Пусть на вход объекта, имеющего непрерывную передаточную функцию
![]() ,
,
поступает единичное ступенчатое воздействие x(t) = 1(t). Тогда переходная характеристика объекта имеет вид:
y(t) = 3 – 2.25e-0.5t.
Произведем измерение входа x(t) и выхода y(t) с периодом дискретизации Dt=1.5 с Считаем значения предельных допускаемых погрешностей средств измерения известными: ex=0.1% и ey=0.1% от верхнего предела измерений. Так, получаем значения ex=0.001, и ey=0.003.
На основе полученных значений рассчитаем идентифицирующую матрицу:
|
|
0 |
1 |
… |
|
0 |
[0.999000, 1.001000] |
[0.999000, 1.001000] |
… |
|
1 |
[0.747025, 0.752975] |
[1.934200, 1.94015] |
… |
|
2 |
[-1.599167, -1.566742] |
[-2.349854, -2.311497] |
… |
|
3 |
[1.068910, 1.151731] |
[1.587336, 1.682430] |
… |
|
4 |
[-0.128530, 0.121617] |
… |
… |
|
… |
… |
… |
… |
Все элементы четвертой строки матрицы содержат в себе число 0, поэтому вычисление следующих строк матрицы на этой строке прекращается.
Нулевой столбец матрицы порождает непрерывную дробь:
 .
.
Правила интервальной арифметики позволяют преобразовать непрерывную дробь к дробно-рациональному выражению:
![]()
Таким образом, получена
интервальная дискретная передаточная функция объекта в виде
дробно-рационального выражения.
Переходя во временную область, получаем интервальную дискретную модель переходной характеристики:
y(n) = [0.746279, 0.753729]x(n) +
+ [0.797705, 0.868093]x(n-1) +
+ [0.415011, 0.530257]y(n-1),
n = 0, 1, 2, …
Выделим граничные функции:
ymin(n) = 0.746279x(n) + 0.797705x(n-1) +
+ 0.415011y(n-1),
n = 0, 1, 2, …
ymax(n) = 0.753729x(n) + 0.868093x(n-1) +
+ 0.530257y(n-1),
n = 0, 1, 2, …
Таким образом,
интервальное задание исходных данных позволяет сохранить эффективность и работоспособность
метода SP-идентификации.
В то же время интервальная неопределенность исходных данных уменьшает интервал
периодов дискретизации, обуславливающих отношение эквивалентности моделей, т.
е. можно утверждать [2], что в данном случае отношение эквивалентности грубее,
чем отношение эквивалентности в детерминированном случае. Практика показала,
что применение способа SP-идентификации
значительно повышает качество и эффективность цифровых систем контроля,
диагностики и управления. Это связано с тем, что уменьшается неточность
результатов, способ просто реализуется в цифровых системах, приводит к
эквивалентной перестройке алгоритмического обеспечения (перенастраиваемость),
ориентируется на максимально возможный период дискретизации
Литература
1.
Нариньяни А. С. Не-факторы:
неточность и неопределенность – различие и взаимосвязь / «Известия Академии
наук. Теория систем управления», №5. – 2000. – С. 44-56.
2.
Кочубиевский Н. Д. Системы нагружения
для исследования и испытаний машин и механизмов. – М.: Машиностроение, 1985. –
224 с.
3.
Карташов В. Я.
Непрерывные дроби (определения и свойства). Учебное пособие. – Кемерово,
Кемеровский госуниверситет. – 1999. – 88 с.
4.
Шокин Ю. И. Интервальный анализ. – Новосибирск: Наука,
1981.