1. Состояние рассматриваемого вопроса
Задача прогнозирования потребления электрической энергии на уровне региональных энергосистем весьма актуальна в настоящее время.
В силу того, что некоторые влияющие на электропотребление факторы имеют случайный характер (например, суммарная нагрузка потребителей, температура окружающей среды и др.), для решения указанных задач применяются методы, основанные на теории вероятностей и математической статистике. К этим методам можно отнести выборочный метод, факторный анализ, планирование эксперимента, однако самым распространенным методом является регрессионный анализ.
Регрессионный анализ основан на критерии наименьших квадратов и позволяет оценивать и прогнозировать электропотребление в зависимости от сколь угодно большого числа воздействующих факторов [1]. Однако для построения регрессионной модели необходимо иметь большой объем исходной статистической информации о воздействующих факторах и электропотреблении.
В некоторых случаях по разным причинам информации об электропотреблении может быть недостаточно, или она может иметь интервальный или нечеткий характер, то есть представляться в виде интервальных значений или функций принадлежности [2]. В качестве возможных причин такой неопределенности можно назвать следующие:
- неодновременность снятия показаний регистрирующих электропотребление приборов;
- несовершенство систем учета электропотребления;
- невозможность достоверного определения коммерческой составляющей потерь электроэнергии;
- влияние температуры окружающей среды на пропускную способность и потери электроэнергии в линиях электропередачи и др.
В подобных ситуациях применение традиционных методов оценки и прогнозирования электропотребления становится весьма затруднительным, что дает возможность использование подходов, предназначенных для решения описываемых задач в условиях неопределенности. Одним из таких методов является предлагаемый авторами нечеткий регрессионный анализ интервальных данных, позволяющий решать задачи прогнозирования и давать оценки интересующих параметров при интервальном характере зависимых переменных.
2. Нечеткий
регрессионный анализ интервальных данных
В соответствии с этим методом, коэффициенты уравнения регрессии
представляются в нечетком виде при помощи функции принадлежности, задающих конкретному значению коэффициента соответствующую
принадлежность из интервала [0, 1]. Такая форма представления применяется в
силу того, что определить закон распределения вероятностей в данном случае
затруднительно. Нечеткий регрессионный анализ с только одной независимой
переменной X имеет следующую
двухкоэффициентную модель регрессии:
,
(1)
где ~ обозначает символ нечеткости, 
является нечетким
коэффициентом пересечения, а 
является нечетким
коэффициентом наклона линии регрессии. Нечеткий параметр 
выражен как
симметричная треугольная функция принадлежности, которая состоит из нечеткого
центра mj и половины
нечеткого основания cj [3 - 5].
Выбор симметричного треугольного типа функции принадлежности обоснован
его простотой. Однако возможно использование и таких функций принадлежности,
как асимметричный треугольник, трапеция и др.
Коэффициенты нечеткой регрессии определены таким образом, что все
нечеткие выходные данные находятся в пределах нечеткой регрессионной модели.
Характерной особенностью данного метода является возможность
использования в качестве исходных данных об интересующем параметре не только
интервальных значений, но и четких.
Для построения нечеткой регрессионной зависимости используется
формулировка задачи линейного программирования, чтобы определить нечеткие
коэффициенты регрессии 
и 
, которая представлена в следующем виде
. (2)
При ограничениях 
для i = от 1 до n, (3)
для i = от 1 до n, (4)
где 
и 
- нижние и верхние
пределы для каждого нечеткого значения соответственно (очевидно, что при точном
задании исходных данных эти пределы равны друг другу, то есть 
). Целевая функция в выражении (2) является результатом
минимизации полного нечеткого разброса. Ограничения (3) и (4) используются для
заключения всех наблюдаемых данных в пределах нечеткой регрессионной модели.
Вышеупомянутая формулировка линейного программирования является задачей
минимизации согласно Ishibuchi [3, 4]. Кроме того, данный метод можно
распространить и на множественные модели регрессии, что представлено в виде
. (5)
При ограничениях с0 ³ 0, с1 ³0, …, сk ³0,
для i = от 1 до n,
(6)
для i = от 1 до n,
(7)
где k – количество
коэффициентов регрессии, n – объем выборки исходных данных.
Важной
особенностью нечетких регрессионных моделей является то, что данные выражения
зависят не от объема выборки исходных данных, а от максимального и минимального
разбросов интервальных значений. Данное утверждение будет проиллюстрировано в
разделе результатов нечеткого
регрессионного анализа.
3. Нечеткий
регрессионный анализ электропотребления в зависимости от температуры окружающей
среды
3.1.
Постановка задачи
В качестве иллюстрации применения предлагаемого метода рассматривается задача оценки и прогнозирования электропотребления Новосибирской энергосистемы в зависимости от температуры окружающей среды в осенне-зимний период.
Как известно, сопротивление
проводов линий электропередачи зависит от температуры провода, которая, в свою
очередь, зависит от температуры окружающей среды [6]. Следовательно, с
изменением температуры окружающей среды происходит изменение пропускной
способности линий электропередачи, а также изменение потерь мощности и энергии
в линиях.
Кроме того, в осенне-зимний
период снижение температуры воздуха приводит к существенному увеличению
использования электронагревательной аппаратуры населением, что вызывает рост
нагрузок и, соответственно, сказывается на уровне и графике электропотребления.
В силу указанных причин
зависимость электропотребления от температуры окружающей среды представляет
большой интерес.
Авторами была
проанализирована динамика изменения электропотребления региональной
энергосистемы в зависимости от температуры окружающей среды в осенне-зимний
период за пять последних лет.
При изменении значений
температуры от 0 до –40 °С выборка исходных
данных составила 36 точек, так как некоторые значения температуры не были
зафиксированы в течение рассмотренного периода.
Удалось установить, что при
одинаковых значениях температуры наблюдались различные значения
элеткропотребления, то есть при точных значениях Х (абсолютная величина
температуры окружающей среды, °С) наблюдаются интервальные
значения Y (потребление
электроэнергии, тыс. кВт*ч). Таким образом, исходные данные о суточном
потреблении электроэнергии имеют интервальный характер. Причем ширина интервала
непостоянна, как и количество точек Y при фиксированном Х.
Эта особенность служит обоснованием применения нечеткого регрессионного анализа
зависимости электропотребления от температуры окружающей среды.
3.2. Результаты применения нечеткого регрессионного анализа для прогнозирования электропотребления с учетом температуры окружающей среды
Авторами произведено построение нечетких регрессионных моделей для трех случаев, когда объем выборки исходных данных составляет 36 точек, 18 точек и 6 точек соответственно. Характерной особенностью всех выборок является наличие точек с максимальными и минимальными разбросами интервальных данных суточного потребления электроэнергии.
Во всех трех случаях
получена одинаковая модель нечеткой интервальной регрессии, имеющая вид
(8)
На рис. 1 показана нечеткая регрессионная модель зависимости суточного электропотребления от температуры окружающей среды при объеме выборки n = 36, а на рис. 2 проиллюстрирована модель при n = 6. Как несложно заметить, на всех трех графиках границы полученных моделей одинаковы.
Полученные результаты свидетельствуют о том, что для построения интересующей регрессионной зависимости достаточен минимальный объем выборки, содержащий максимальный и минимальный разбросы интервальных данных. При этом качество предсказательной способности получаемой нечеткой регрессионной модели не ухудшается с уменьшением выборки.
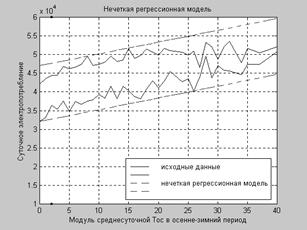
Рис. 1. Зависимость суточного
электропотребления от температуры окружающей среды при n = 36.
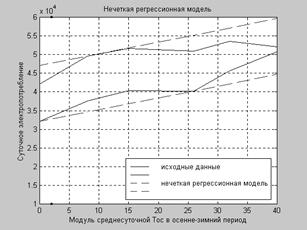
Рис. 2. Зависимость суточного
электропотребления от температуры окружающей среды при n = 6.
Можно также отметить, что моделирование полученных зависимостей производилось в пакете математических программ MATLAB.
4. Результаты и выводы
В результате проведенных исследований
можно сделать следующие основные выводы.
1. При исходной информации об
интересующем параметре (в данном случае – суточном электропотреблении),
заданной интервально, для построения регрессионных моделей целесообразно
использовать нечеткий регрессионный анализ.
2. Нечеткий регрессионный анализ
вполне может применяться и в случае точного задания исходных данных. При этом
наличие интервального разброса полученных результатов в данном методе позволит
учесть неопределенность исходной информации и может заменить доверительный
интервал стандартной линии регрессии. Иначе говоря, нечеткий регрессионный
анализ имеет некоторую универсальность относительно вида исходных данных
исследуемого зависимого параметра.
3. Нечеткая регрессионная модель, в
отличие от стандартной регрессии, не зависит от объема выборки. Модель в этом
случае зависит от разброса исходных данных. Этот факт позволяет существенно упростить
процесс построения моделей путем сокращения выборки исходных данных. При этом
достоверность полученных результатов прогнозирования суточного
электропотребления не уменьшается.
Все вышесказанное, по мнению
авторов, свидетельствует о возможности и эффективности применения нечеткого
регрессионного анализа для задач оценки и прогнозирования электропотребления
энергосистем.
Литература
[1]. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Статистика. – 1973. 392 с.
[2]. Заде Л.А. Понятие лингвистической переменной и его применение к
принятию приближенных решений. - М.: Мир. - 1976. 168 с.
[3]. Yun-Hsi O. Chang, Bilal M. Ayyub Fuzzy regression methods - a comparative assessment.// Fuzzy Sets and Systems, Vol. 119 (2), 2001. p. 187 – 203.
[4]. Манусов В.З., Могиленко А.В. Методы оценивания потерь электроэнергии в условиях неопределенности. // Электричество, 2003. №3. 2 – 8 с.
[5]. Манусов В.З., Могиленко А.В. Прогнозирование электропотребления в энергосистемах при неопределенности в исходной информации. // Материалы докладов восьмой всероссийской научно – техническая конференции «Энергетика: экология, надежность, безопасность» часть I. – Томск: ТПУ. – 2002. 74 – 77 с
[6]. Поспелов Г.Е., Сыч Н.М. Потери мощности и энергии в электрических
сетях. М.: Энергоиздат. – 1981. 216 с.