Нейронные сети и информационные системы с
нечеткой логикой имеют свои специфические особенности: с одной стороны,
возможность обучения, а с другой, процесс решения задач системами с нечеткой
логикой достаточно прозрачен для объяснения получаемых выводов. Объединение
двух названных подходов в нечетких НС позволяет сочетать достоинства нейросетевых
вычислительных средств и нечетких логических систем, опирающихся на априорный
опыт в виде заданной системы нечетких предикатных правил.
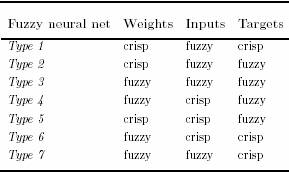
Как следует из опыта разработки нечетких НС (таб. 1) [1] для целей классификации реализуют
нейро-нечеткие сети (FNN) типа 1, которые решают
задачу отнесения нечеткого входного вектора к четкому классу, а FNN типов 2, 3 и
4 применяют для построения нечетких систем, основанных на системе нечетких
правил вывода
Таблица 1
Рассмотрим подход к организации нейро-нечеткого
классификатора, использующего механизм нечеткого логического вывода при решении
задачи классификации нечетких входных векторов (Inputs) нейронной сетью с
нечеткими связями.
Механизм нечеткого логического вывода основан на
базе знаний, формируемой специалистами предметной области (экспертами) в виде
системы нечетких предикатных правил, например:
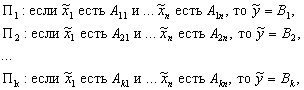 где
где 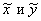 - нечеткие входная
переменная и переменная вывода, а
- нечеткие входная
переменная и переменная вывода, а 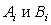 - соответствующие функции принадлежности.
- соответствующие функции принадлежности.
Для реализации системы нечетких предикатных
правил нейро-нечеткий классификатор (аналогично процедуре логического вывода) должен
выполнять следующие действия:
·
введение нечеткости (fuzzification) - по функциям принадлежности, заданным на области определения предпосылок,
исходя из фактических значений нечетких переменных 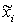 , определять степень истинности каждой предпосылки;
, определять степень истинности каждой предпосылки;
·
логический вывод - по степени истинности предпосылок формировать
заключения по каждому из правил, образующие нечеткое подмножество для каждой
переменной вывода по каждому из правил;
·
композиция - полученные на предыдущем этапе нечеткие
подмножества для каждой переменной вывода по всем правилам объединять с целью
формирования нечеткого подмножества для всех переменных вывода.
Пусть задано полное пространство предпосылок 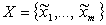 и полное пространство
заключений
и полное пространство
заключений 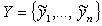 . Между
. Между 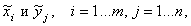 существуют нечеткие
причинные отношения
существуют нечеткие
причинные отношения 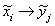 , которые можно представить в виде матрицы
, которые можно представить в виде матрицы 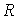 с элементами
с элементами
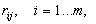
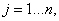 а предпосылки и заключения - как нечеткие
множества
а предпосылки и заключения - как нечеткие
множества 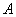 и
и 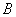 на пространствах
на пространствах 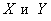 , отношения которых можно представить в виде:
, отношения которых можно представить в виде: 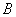 =
=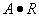 , где · - операция композиции,
например, max-min-композиция.
, где · - операция композиции,
например, max-min-композиция.
В нечетких логических выводах знания эксперта 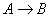 отражает нечеткое отношение
отражает нечеткое отношение 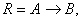 (нечеткое причинное отношение
предпосылки и заключения), где операция ®
соответствует нечеткой импликации. Нечеткое отношение
(нечеткое причинное отношение
предпосылки и заключения), где операция ®
соответствует нечеткой импликации. Нечеткое отношение 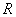 можно рассматривать
как нечеткое подмножество прямого произведения
можно рассматривать
как нечеткое подмножество прямого произведения 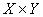 полного множества
предпосылок
полного множества
предпосылок 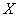 и заключений
и заключений 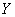 , а процесс получения нечеткого результата вывода
, а процесс получения нечеткого результата вывода 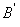 по предпосылке
по предпосылке 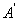 и знаниям
и знаниям 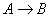 можно представить в
виде композиционного правила:
можно представить в
виде композиционного правила: 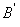 =
=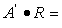
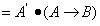 .
.
В полном пространстве предпосылок 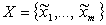 максимально число входных
нечетких векторов задается всевозможными сочетаниями координат
максимально число входных
нечетких векторов задается всевозможными сочетаниями координат 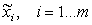 . Каждому входному вектору из пространства X можно поставить в
соответствие нечеткий ФН нейро-нечеткого
классификатора, выполняющий операцию логического вывода, например, min.
Отображение множества результатов логического вывода в полное пространство
заключений
. Каждому входному вектору из пространства X можно поставить в
соответствие нечеткий ФН нейро-нечеткого
классификатора, выполняющий операцию логического вывода, например, min.
Отображение множества результатов логического вывода в полное пространство
заключений 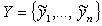 можно реализовать
посредством операции композиции, и каждому выходному вектору из пространства Y можно поставить в соответствие
нечеткий ФН нейро-нечеткого классификатора, выполняющий
операцию, к примеру, max.
можно реализовать
посредством операции композиции, и каждому выходному вектору из пространства Y можно поставить в соответствие
нечеткий ФН нейро-нечеткого классификатора, выполняющий
операцию, к примеру, max.
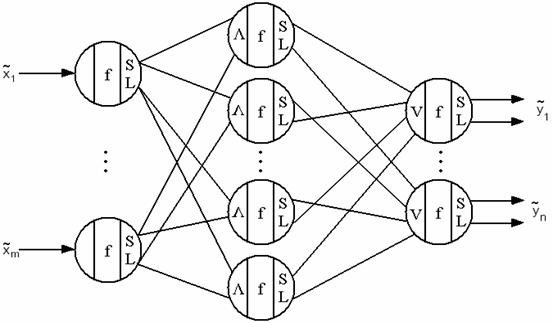
Нейро-нечеткий классификатор m-мерных нормализованных
векторов Х с нечеткими координаторами 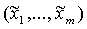 будем представлять в
виде трехслойной нечеткой нейронной сети (рис. 1), в которой:
будем представлять в
виде трехслойной нечеткой нейронной сети (рис. 1), в которой:
- первый слой содержит m, по числу координат
входного вектора, нечетких нейронов с комплементарными нечеткими связями, формирующих
m пар нечетких высказываний
(НВ) вида:
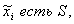
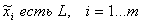 ;
;
- средний слой содержит до 2m нечетких нейронов с
комплементарными нечетким связями, выполняющих операцию логического вывода
(например, min) над сочетаниями
нечетких высказываний первого слоя НС с целью формирования
системы нечетких классификационных заключений;
- выходной слой содержит n, по числу координат
выходного вектора, нечетких нейронов с комплементарными нечетким связями, выполняющих
операцию композиции (например, max)
над нечеткими классификационными заключениями второго слоя НС
для формирования n-мерных векторов Y выходных нечетких
заключений 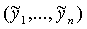 .
.
Нечеткие нейроны первого слоя в соответствии с заданным
типом функции принадлежности f
формируют комплементарные пары значений истинности для входных нечетких переменных
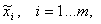 координат входного
вектора Х. Координаты входного вектора нормализованы путем деления на значение
ядра нечеткой переменной. При заданном значении координаты вектора Х
на отрезке области определения каждой паре значений истинности входных нечетких
переменных соответствуют значения ординат функций принадлежности S (small)
и L (large), которые в сумме дают
1. То есть каждый нечеткий формальный нейрон первого слоя реализует пару «частично
противоположных» нечетких высказываний, которые через комплементарную пару
нечетких связей подаются на средний слой НС.
координат входного
вектора Х. Координаты входного вектора нормализованы путем деления на значение
ядра нечеткой переменной. При заданном значении координаты вектора Х
на отрезке области определения каждой паре значений истинности входных нечетких
переменных соответствуют значения ординат функций принадлежности S (small)
и L (large), которые в сумме дают
1. То есть каждый нечеткий формальный нейрон первого слоя реализует пару «частично
противоположных» нечетких высказываний, которые через комплементарную пару
нечетких связей подаются на средний слой НС.
Нечеткая
связь на выходе ФН представляет собой совокупность взвешенных межнейронных
связей, веса которых отражают распределение истинности в нечетком множестве,
соответствующем некоторой функции принадлежности [3]. Пара функций
принадлежности, например S и L
образуют две нечеткие связи, составляющие одну комплементарную нечеткую связь.
Если
средний слой нечеткой НС содержит максимальное число
нечетких нейронов «И», то промежуточный вектор нечетких заключений будет
содержать все возможные нечеткие классификационные заключения, которые могут
следовать из всех возможных векторов входных нечетких посылок.
Выходной
слой нечеткой НС образован из нечетких нейронов «ИЛИ»
(по числу нечетких заключений 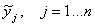 ) и формирует вектор выходных нечетких заключений в
соответствии с заданной экспертами системой нечетких предикатных правил.
) и формирует вектор выходных нечетких заключений в
соответствии с заданной экспертами системой нечетких предикатных правил.
Последующее
обучение нейро-нечеткого классификатора может производиться с использованием алгоритмов
адаптации нейро-нечетких сетей, в частности с использованием механизма нечеткой
межнейронной связи [4]. Обучение нейро-нечеткого классификатора на наборе векторов
обучающей выборки позволит выявить возможную противоречивость исходной системы
нечетких предикатных правил и устранить из структуры нейронной сети незначащие
связи (неточные заключения из исходной
системы нечетких предикатных правил) [5].
Область
применения адаптивного нейро-нечеткого классификатора включает активно
развивающиеся отрасли информационных технологий, такие как информационная
безопасность (information safety), хранилища данных (data
warehouse), системы извлечения знаний из больших объемов
первичной информации (data mining
and knowledge engineering).
Литература
1.
Fuller R. Neural Fuzzy
Systems. – Abo: Abo Akademi University, 1995. 252 p.
2. Круглов В. В., Борисов В. В. Искусственные нейронные
сети. Теория и практика.- 2-е изд., стереотип. – М.: Горячая линия - Телеком,
2002.
3. Нестерук Г.Ф., Куприянов М.С., Нестерук Л.Г. О реализации
интеллектуальных систем в нечетком и нейросетевом базисах
// SCM’2003. - СПб, 25 - 27 июня 2003. (в данном сборнике тезисов докладов).
4. Nesteruk G. Ph.,
Kupriyanov M. S. Neural-fuzzy systems with fuzzy links // SCM’2003. - СПб, 25 - 27 июня 2003. (в данном сборнике тезисов докладов).
5. Negneyitsky M. Artificial
intelligence: a guide to intelligent systems. Addison-Wesley, 2002.

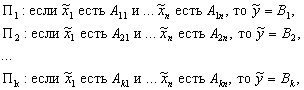 где
где ![]() - нечеткие входная
переменная и переменная вывода, а
- нечеткие входная
переменная и переменная вывода, а ![]() - соответствующие функции принадлежности.
- соответствующие функции принадлежности.![]() , определять степень истинности каждой предпосылки;
, определять степень истинности каждой предпосылки;![]() и полное пространство
заключений
и полное пространство
заключений ![]() . Между
. Между ![]() существуют нечеткие
причинные отношения
существуют нечеткие
причинные отношения ![]() , которые можно представить в виде матрицы
, которые можно представить в виде матрицы ![]() с элементами
с элементами
![]()
![]() а предпосылки и заключения - как нечеткие
множества
а предпосылки и заключения - как нечеткие
множества ![]() и
и ![]() на пространствах
на пространствах ![]() , отношения которых можно представить в виде:
, отношения которых можно представить в виде: ![]() =
=![]() , где · - операция композиции,
например, max-min-композиция.
, где · - операция композиции,
например, max-min-композиция.![]() отражает нечеткое отношение
отражает нечеткое отношение ![]() (нечеткое причинное отношение
предпосылки и заключения), где операция ®
соответствует нечеткой импликации. Нечеткое отношение
(нечеткое причинное отношение
предпосылки и заключения), где операция ®
соответствует нечеткой импликации. Нечеткое отношение ![]() можно рассматривать
как нечеткое подмножество прямого произведения
можно рассматривать
как нечеткое подмножество прямого произведения ![]() полного множества
предпосылок
полного множества
предпосылок ![]() и заключений
и заключений ![]() , а процесс получения нечеткого результата вывода
, а процесс получения нечеткого результата вывода ![]() по предпосылке
по предпосылке ![]() и знаниям
и знаниям ![]() можно представить в
виде композиционного правила:
можно представить в
виде композиционного правила: ![]() =
=![]()
![]() .
.![]() максимально число входных
нечетких векторов задается всевозможными сочетаниями координат
максимально число входных
нечетких векторов задается всевозможными сочетаниями координат ![]() . Каждому входному вектору из пространства X можно поставить в
соответствие нечеткий ФН нейро-нечеткого
классификатора, выполняющий операцию логического вывода, например, min.
Отображение множества результатов логического вывода в полное пространство
заключений
. Каждому входному вектору из пространства X можно поставить в
соответствие нечеткий ФН нейро-нечеткого
классификатора, выполняющий операцию логического вывода, например, min.
Отображение множества результатов логического вывода в полное пространство
заключений ![]() можно реализовать
посредством операции композиции, и каждому выходному вектору из пространства Y можно поставить в соответствие
нечеткий ФН нейро-нечеткого классификатора, выполняющий
операцию, к примеру, max.
можно реализовать
посредством операции композиции, и каждому выходному вектору из пространства Y можно поставить в соответствие
нечеткий ФН нейро-нечеткого классификатора, выполняющий
операцию, к примеру, max.