В работе рассматривается один из принципиальных вопросов логических формализмов: соответствие формализма содержательному пониманию логических связок, в частности, одноместной связки. Однако работа адресована в первую очередь не логикам, а тем, для кого логика – средство для решения практических задач.

В филологии и в логике рассматриваются совместимые и несовместимые понятия. Несовместимые – понятия, объёмы которых не совпадают, т.е. не имеют общих элементов. Нeсовместимые понятия разделяются на понятия: несравнимые, противоречащие и противоположные. Несравнимые понятия– понятия, которые не имеют ближайшего общего родового понятия (например, "аромат" и "квадрат"). Противоречащие понятия – несовместимые понятия, между которыми нет среднего, третьего, промежуточного понятия и которые исключают друг друга. Иначе такие понятия называются контрадикторными (например, "белый" и "небелый"). Противоположные понятия – несовместимые понятия, между которыми, возможно третье, среднее понятие и которые не только отрицают друг друга, но несут в себе нечто положительное взамен отрицаемого в противопоставимом понятии (например, "белый" и "чёрный"). Иначе такие понятия называются контрарными. Контрадикторными и контрарными могут быть не только понятия, но и суждения.

Понятия (суждения), находящиеся в контрадикторном отношении, одновременно не могут быть ни истинными, ни ложными; одно и только одно из них истинно, а другое обязательно ложно. Если известно, что понятие (суждение) истинно, то контрадикторное ему понятие (суждение) ложно; и наоборот, если известно, что понятие ложно, то контрадикторное ему понятие истинно. Эту связь между контрадикторными понятиями (суждениями) можно выразить посредством таблицы:

	ù
И	Л
Л	И

Табл. 1.

Понятия (суждения), находящиеся в контрарном отношении, вместе одновременно не могут быть истинными (если одно истинно, то другое непременно ложно), но могут быть оба одновременно ложными.

Итак, противоположности в широком смысле слова (иначе, оппозиции) формально могут быть двух типов. Для наглядности их можно изобразить с помощью рисунков. Возьмём контрадикторные понятия "белый", "небелый" и контрарные понятия "белый", "чёрный". Им соответствуют рисунки:

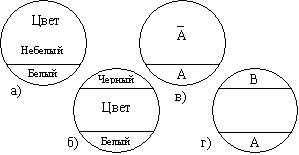Рис. 1.

Понятно, формально одно из контрарных понятий является частным случаем одного из контрадикторных понятий (в нашем примере понятие "черный" входит в число понятий, объединённых понятием "небелый"), а контрадикторные – частным случаем контрарных, когда множество промежуточных понятий пусто.

У обеих оппозиций (контрадикторных, контрарных) есть аспекты лингвистические и логические. Мы коснёмся только вторых. Прежде всего отметим, что они между собой находятся в контрадикторном отношении. Каждая конкретная пара оппозиций попадает либо в число контрадикторных, либо – контрарных. Между ними, т.е. между двумя понятиями оппозиций, нет среднего члена, нет промежуточного понятия. Между оппозициями, вообще, либо есть средний член, либо его нет, нечто промежуточное невозможно. Рисунку 1в соответствует формула:

~U, (1)

где U – внешний круг, а и – его части. Очевидно, идею контрадикторности можно пояснить рисунком, в котором внешний круг заменен прямоугольником:

Рис. 2.

Но ту же идею дополнительности можно иллюстрировать и отрезком:

Рис. 3.

Если считать, что принимает значения из двухэлементного множества {0,1}, то справедливо равенство:

+ù=1, (2)

в котором ù задаётся таблицей, аналогичной таблице 1, с тем лишь отличием, что в ней вместо букв И и Л стоят числа 1 и 0.

Контрадикторные оппозиции рассматриваются в классическом исчислении высказываний. Видимо, понятно, что контрадикторные и контрарные оппозиции не могут быть предметом рассмотрения одного и того же исчисления.

Какой должна быть логическая система, в которой фигурирует контрарная оппозиция? Думается, понятно, что контрарность не может быть описана не только средствами классического исчисления высказываний, но и, вообще, средствами двузначной логики.

Чтобы составить более полное представление о контрарной оппозиции, обратим внимание на то, что из закона противоречия следуют следующие правила:

1. Контрарные понятия об одном и том же классе предметов, взятых в одно и то же время и в одном и том же отношении:

1.1. Не могут быть сразу оба истинными;

1.2. Могут быть сразу оба ложными.

2. Из истинности одного из контрарных понятий обязательно следует ложность другого контрарного понятия.

3. Из ложности одного из контрарных понятий логически не следует ни истинность, ни ложность другого противоположного понятия.

Приведённые правила сформулированы с позиций двузначной логики. В ней термины "неистинность" и "ложность" означают одно и то же. В недвузначных логиках это не так. Слово "неистинность" в них вовсе не означает "ложность". Употребление термина "неистина" позволяет в недвузначных логиках формулировать утверждения с сохранением их бинарности. Утверждение либо истинно, либо неистинно, но при этом оно может не быть ложным. Таким образом, можно утверждение, справедливое в двузначной логике, переформулировать в утверждение, справедливое в недвузначных логиках.

Правила, вытекающие из закона противоречия, в недвузначном случае могут быть сформулированы так:

1.1. Не могут быть сразу оба истинными;

1.2.Могут быть сразу оба неистинными.

2. Из истинности одного из контрарных понятий обязательно следует ложность другого контрарного понятия.

3. Из неистинности одного из контрарных понятий логически не следует ни истинность, ни ложность другого контрарного понятия.

Посмотрим, как контрадикторное отношение, по природе своей сугубо бинарное, может быть распространено на более широкое множество истинностных значений, чем множество из двух чисел {0,1}. Такое распространение осуществил Мак-Нотон в 1951 г. Он в качестве истинностных значений рассматривает не множество {0, l}, а отрезок [0, 1], сохраняя связь между и ù посредством уравнения (2).

При этом в уравнении:

+ ù = 1, (3)

где и ù берутся из множества [0, l], сохраняется та же идея дополнительности, которая формализуется с помощью эквивалентности (I). Если эквивалентность (I) выражает качественную зависимость между дополняющими друг друга множествами, то в уравнении (3) присутствует та же идея, пополненная числами, которые ставятся в соответствие дополняющим друг друга множествам. Универсум, обозначенный посредством U, символизирует в (1) нечто единое и постоянное. Ему приписывается число 1, а частям универсума – части единицы, дающие в сумме единицу. Так получается уравнение (3). В нём и ù говорят о том, в каком соотношении универсум поделён на части. В силу близкой аналогии, усматриваемой в уравнении (3) и эквивалентности (1), кажется естественным уравнение (3) называть уравнением дополнительности.

Уравнение:

+ ù = C, (4)

в котором С – любое число, а и ù – две его части, очевидное обобщение yравнения (3). Уравнение (4), как и уравнение (3), в некотором смысле аналог эквивалентности (1). В нём, думается, идея дополнительности нисколько не пострадала, поскольку остаются в силе все соображения, высказанные относительно дополнительности. В (4) константа С ставится в соответствие универсуму U, входящему в (1). Уравнение (4) также будем называть уравнением дополнительности.

Эквивалентность (1) ни в коей мере не отражает идеи присутствия промежуточного третьего члена в отношении контрарности. А потому и ù, фигурирующие в уравнении (4) – аналоге эквивалентности (1), никак нельзя признать связанными отношением контрарности. Думается, уравнение (4) является наиболее общей формой выражения идеи дополнительности средствами уравнений. В нём в явном виде оценивается соотношение присутствия двух противоречивых качеств, оценивается степень дополнения оппозиций друг другом, а не только фиксируется сам факт дополнения, как это имеет место в эквивалентности (1).

Идея дополнительности и уравнение дополнительности используются в теории вероятностей. Действительно, из теоремы сложения следует:

P()+P() = 1,

где и – противоположные события, дополняющие друг друга, а P() и P() – числа, которые ставятся им в соответствие. Эти числа P() и P() не характеризуют что-то промежуточное между событиями и . Между этими событиями не предполагаются какие-либо промежуточные события. В теории вероятностей объединяются две идеи: идея контрадикторной оппозиции и идея континуальности оценок. Событие не просто может быть или не может быть (дискретный двузначный взгляд на события), но может быть (или не быть) с оценкой из отрезка [0,1]. Непрерывность в оценках, однако, ни в коей мере не изменяет контрадикторного отношения между понятиями, которые соответствуют событиям и . В теории вероятностей поле событий подчиняется законам двузначной классической логики, а оценки – уравнению дополнительности. Думается, есть основания говорить о гармонии в теории вероятностей между количественной стороной и качественной, отражаемой полем событий.

Отметим, что логика любого ранжирования (о каких бы задачах, какой бы области ни шла речь) основана на использовании градуальной оппозиции, т.е. на предположении, что между крайними (предельными) понятиями есть средние, расположенные между ними. Какие-то из средних ближе, а какие-то дальше от предельных. Логика, используемая при ранжировании, – логика контрарных отношений. Теория вероятностей не относится к числу таких логических систем.

Чтобы отличать контрадикторное отношение от контрарного, введем обозначение , a для пары, связанной контрарно, сохранив обозначения , ù для пары, связанной контрадикторно. Если в контрарной паре , a оба элемента равноправны, то в контрадикторной паре , ù равноправия нет. В контрадикторной паре А – элемент, а ù неопределенное множество. Например, в контрадикторной паре "белое", "небелое" первый элемент – конкретный цвет, а второй – неопределенное множество, имеющее явно отрицательный характер. В контрарной же паре " белое", " черное" оба элемента – конкретные цвета, содержащие в себе в равной мере положительное содержание. Можно сказать, что нечто, обозначенное посредством Z, ближе к , чем к a, но абсурдно говорить о том, что Z ближе к , чем к ù. Z, будучи отличным от А, является элементом множества ù, а потому не может быть дальше или ближе от самого себя.

Чтобы не складывалось мнение, что рассматриваемые понятия контрадикторности и контрарности далеки от реалий разговорного языка, еще раз обратимся к примерам. Будем оценивать высказывания по двоичной системе: истина, ложь.

Примеры

1.Стена белая.

Стена небелая.

2. Все сотрудники ЦНИ – блондины.

Некоторые сотрудники ЦНИ не являются блондинами.

3.Веселый человек.

Грустный человек.

Ничего определенного сказать нельзя (может быть И, может быть Л).

4. Все сотрудники ЦНИ – блондины.

Ни один сотрудник ЦНИ не является блондином.

Ничего определенного сказать нельзя (может быть И, может быть Л).

Видим, в языке действительно присутствуют оппозиции двух типов. Примеры 1, 2 иллюстрируют контрадикторные оппозиции, а примеры 3, 4 – контрарные.

ЦНИ Санкт-Петербургского государственного политехнического университета

При этом в уравнении:

Уравнение:

Примеры

Стена небелая.