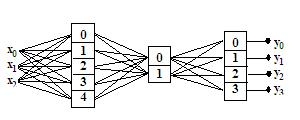Возможны два пути технической реализации больших
нейронных сетей: 1) – создание линейки нейрочипов, в которой каждая микросхема
соответствует алгоритму определенной размерности; 2) – построение
реконфигурируемых СБИС[1] способных изменять
свою внутреннею структуру и топологию связей в зависимости от размерности
данных. Технология СБИС накладывает ряд ограничений
на реализацию нейронных сетей больших масштабов к ним относятся:
регулярность структуры и топологических связей, рекурсивность, локализованность
передачи данных. Среди многослойных алгоритмических структур наиболее полно поставленным
требованиям удовлетворяют регулярные ядерные слабосвязанные сети [1]. В нейронных
сетях данного типа в каждом нейронном слое можно выделить группы нейронов с
непересекающимися рецепторными полями – нейронные ядра. Нейронное ядро по
существу представляет собой однослойный персептрон и на структурном уровне
характеризуется размерностью рецепторного поля и числом входящих в него нейронов.
В регулярных сетях все ядра в пределах слоя имеют одинаковые размерности. Характерной
особенностью слабосвязанных сетей является отсутствие параллельных путей при полных связях между вершинами терминальных
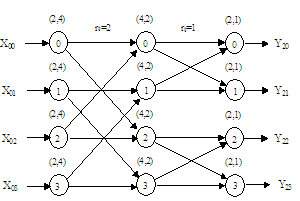
слоев. На рис. 1 структурное представление слабосвязанной нейронной сети, где
вершинами графа являются нейронные ядра.
|
Рис. 1. Структурная модель слабосвязанной сети |
В настоящее время не существует строгих методов априорного
выбора структуры сети, и поиск оптимального решения, как правило, осуществляется путем
проб и ошибок. Поэтому любая практическая реализация нейронной сети должна
обладать способностью к реконфигурации структуры и топологии. В минимальном
варианте это может быть изменение размерностей терминальных полей при
сохранении структуры и топологии сети. В общем случае сохраняемыми свойствами
являются только регулярность и слабая связанность сети, все остальные характеристики
подвергаются модификации. В работе [2] был предложен формальный язык, который позволил
разработать методы структурного и топологического синтеза регулярных Быстрых нейронных
сетей (БНС). В данной статье рассматривается расширение данного языка, ориентированное
на описание процедур реконфигурации регулярных сетей общего вида.
Подходящей математической
моделью реконфигурируемой сети может служить модель «класс-объект», получившая
широкое распространение в современных языках программирования. В рамках данной
модели регулярную нейронную сеть будем рассматривать как объект программного
класса. Взаимодействие с объектом реализуется через набор допустимых объектных функций.
Функции класса позволяют изменять структурные и топологические характеристики
нейронной сети, сохраняя при этом свойства регулярности и слабой связанности. В
контексте формального языка набор объектных функций можно рассматривать как порождающую
грамматику, описывающую всевозможные расширения языка, а в контексте объектно–ориентированного
подхода как интерфейс взаимодействия с объектом. В данной статье на примере
двух объектных функций рассмотрены принципы реализации регулярно–реконфигурируемой
нейронной сети.
Семантика формального языка. Практическая ценность
формального языка определяется его семантической интерпретацией, поэтому
рассмотрение языка регулярных сетей целесообразно начать с его семантики. Пусть
некоторое допустимое
слово формального языка. Поставим в соответствие каждой букве 
целое положительное число
, и будем рассматривать букву как символическое обозначение переменной
принимающей целочисленные значения из интервала 
. Слово языка будем интерпретировать как целочисленную функцию,
заданную правилом:
(1)
Порядок следования
аргументов для данной функции имеет существенное значение, поэтому каждое слово
языка представляет собой кортеж, т.е. множество, на котором зафиксирован
линейный порядок. Выражение (1) известно, как правило, представления целого
числа в позиционной системе счисления с несколькими основаниями.
Алфавит языка и грамматика слов. Алфавитом языка будем
считать кортеж неповторяющихся символов 
. Отношение линейного порядка на алфавитном множестве назовем
каноном языка и означим через 
. В сокращенной форме кортеж
алфавита, состоящий из букв с общим родовым именем, записывается в виде 
. Далее используется алфавит с различными типами букв. Каждый
тип буквы определяется его родовым именем (например 
) в этом случае для сокращенной записи алфавита будем
использовать обозначения вида: 
. Пусть алфавит 
состоит из 
букв. Допустимым
словом языка будем считать любой кортеж длиной 
, состоящий из неповторяющихся букв алфавита.
Грамматика предложений. Правила построения
предложений языка определяют порождающую грамматику, которую предлагается использовать
для синтеза регулярных многослойных графов. В начале рассмотрим формальное определение
порождающей грамматики, а затем покажем ее интерпретацию в предметной области.
Слово, в котором порядок
букв согласован с каноном, далее называется каноническим.
Для каждого канонического слова можно построить класс слов, выполняя всевозможные
перестановками его букв. Два подобных класса назовем смежными, если они отличаются одной буквой. Из смежных классов
можно составлять цепочки, в которых каждая пара классов связана общей буквой.
Для множества слов длиной 
максимальная длина
разомкнутой цепочки равна .
В линейных языках каждое
предложение имеет одно начало и один конец. Возможны различные способы
кодирования границ предложения. Мы будем использовать для этой цели вариант
родовых имен. Определим алфавит языка как линейно упорядоченный набор неповторяющихся
букв с двумя видами родовых имен:
,
где отношения 
– определяют состав и порядок букв каждого вида. Число букв каждого
вида будем считать одинаковыми и равным . Таким образом, длина алфавита равна 
. Рассмотрим множество всевозможных слов длиной 
, из которых будем строить предложения. Допустимым предложением
будем считать упорядоченную последовательность слов, каждое из которых является
представителем максимальной цепочки смежных классов. В допустимом предложении
представлены все смежные классы цепочки и каждый класс представлен только одним словом. Длина предложения всегда равна . Последовательность слов в предложении определяется правилом
вывода. Это правило устанавливает начальное слово предложения и описывает связи
между смежными словами. Зафиксируем следующее правило вывода:
§ слова в предложении линейно
упорядочены по числу букв с родовым именем 
;
§ первое слово предложения
выбирается из класса 
и имеет, поэтому нулевое
число вхождений букв с родовым именем .
Каждая цепочка смежных
классов порождает множество однотипных предложений. Среди этого множества
существует единственное предложение, составленное из канонических слов
(каноническое предложение). Все остальные предложения для данной цепочки могут
быть получены из канонического произвольной перестановкой букв
в словах этого предложения. Поэтому достаточно рассматривать порождающую
грамматику только для канонических предложений. Пусть числа 
и 
определяют порядковые
номера двух смежных классов в цепочке. Для класса через 
и 
обозначим линейно
упорядоченные подмножества букв каждого типа, а через 
его каноническое
слово. Тогда правило вывода для канонических предложений можно сформулировать
следующим образом:
. (2)
Причем
Семантическая интерпретация предложений. Поставим в соответствие
каноническому предложению - слойный сетевой граф. Каждое слово с порядковым номером будем интерпретировать
как функциональное правило вычисления номера вершины в слое , определенное
семантикой (1). Будем полагать, что каждой вершине графа отвечает нейронное
ядро. Вершины двух смежных слоев будем считать связанными дугой, если в
поразрядном представлении номеров вершин
,
одноименные
переменные имеют совпадающие значения. На рис. 2 представлено правило
построения семантической интерпретации для предложения:
, (3)
где 
. Можно показать, что построенный граф является слабосвязанной
сетью.
|
Рис. 2. Правило построения структурной модели регулярной сети. |
Топологические
реализации. Каждое нейронное ядро
слоя характеризуется парой
чисел 
, где первое определяет размерность по входу, а второе размерность
по выходу. В регулярных сетях нейронные ядра в пределах слоя структурно-подобны
между собой. Расширим алфавит дополнительными
буквами 
, рассматривая их как имена разрядных переменных с основаниями
. Данные переменные определяют локальные номера терминальных
зажимов нейронных ядер. Последовательно нумеруя все однотипные терминальные
зажимы нейронных ядер в пределах слоя, получим глобальные номера 
. Соответствие между локальными и глобальными номерами
определяет топологическое размещение нейронного ядра в пределах слоя. Регулярность
размещения можно обеспечить, если это соответствие подчинить грамматике формального
языка. Например, для предложения (3) можно выстроить следующую топологию 
для входных полей и 
– для выходных полей.
Граф топологической реализации строится по тем же правилам, что и граф структурной
модели. Словная позиция новых разрядных переменных может быть выбрана
произвольно. Всевозможные перестановки букв в словах
образуют класс различных топологических реализаций, соответствующих одной и той
же структурной модели. Из этого множества можно выбрать топологии, наиболее полно
отвечающие требования СБИС технологии. Правило вывода (2) устанавливает взаимнооднозначные
соответствия 
, 
(возможны и другие варианты),
позволяющие перейти к алфавиту с родовыми именами 
. При этом два топологических предложения можно заменить одним
, (4)
называемое далее топологической траекторией. В данном
предложении первые три слова определяют послойные топологии рецепторных полей,
а последние три слова –топологии аксоновых полей.
Изменение ранга межъядерных связей. Регулярные нейронные сети с рангами связей больше
единицы не принадлежат классу быстрых нейронных сетей. Вычислительная эффективность
для этого класса сетей ниже, чем у однотипных БНС, но они, как правило, обладают лучшей
способностью к обучению, чем последние. На уровне структурных моделей изменение
ранга отражается только в изменении
весов дуг и весов инцидентных к ним вершин, каноническое
предложение, определяющее структуру сети, при этом не изменяется. На рис. 1
показана структурная модель трехслойной нейронной сети с рангами больше
единицы.
Конструкции формального языка позволяют достаточно
просто описывать данный класс сетей и на
уровне топологий. Пусть 
ранги связей в
межслойных переходах. Расширим алфавит языка, разрядными переменными 
, задав их основания следующей таблицей:
.
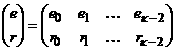Поскольку все связи являются точными и однозначными,
то для каждого межслойного перехода существует взаимно однозначное
соответствие между аксонами и рецепторами смежных слоев так, что.
,
.
Таким образом, топологическая траектория для
рассматриваемого примера будет определяется предложением:
.
Введем объектную функцию 
. Эта функция устанавливает ранг связей (
) в межслойном
переходе (
). Область действия функции может быть расширена и для
граничных переходов, если определить дополнительные разрядные переменные 
и 
. В этом случае функция может быть использована для изменения
размерности терминальных полей, например топологическая траектория
определяет трехслойную сеть
с расширенным входным рецепторным полем.
Интерес представляет
вырожденный вариант когда, основания всех разрядных переменных 
и 
равны единице. В этом
случае каждый слой содержит только одно ядро, а переменные расширения 
определяют размерности
ядер. Например, для топологического
предложения
, где
|
|
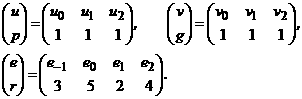
интерпретирующий граф будет иметь вид, показанный на рис 3. Очевидно, что данный граф определяет многослойную полносвязанную нейронную сеть. Таким образом, классическая многослойная сеть принадлежит множеству структурных реализаций реконфигурируемой регулярной сети.
Изменение числа нейронных слоев. Будем
рассматривать алфавитные наборы букв с именами и как два линейных
связанных списка, для которых определены транзакционные функции вставки и удаления.
Обозначим эти функции следующим образом: 
. При выполнении операции вставки добавляются новые разрядные
переменные с именами 
и значениями оснований 
и 
. Все последующие элементы списка изменяют свою нумерацию. При 
и 
операция вставки
добавляет новые разрядные переменные в начало и конец алфавитных списков. Функция
удаляет из списков
переменные с текущим номером и корректирует
позиционные номера последующих переменных. Предполагается, что операции вставки и удаления не изменяют тип порождающей схемы.
Пример. Пусть исходные алфавитные списки переменных определены таблицами
,
а топологическая траектория
– предложением (4) Выполним операцию вставки 
. Новые списки примут вид:
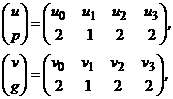
а новое топологическое предложение
будет представлено следующим образом:
.
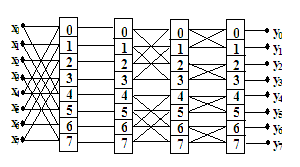
На рис.4 показан интерпретирующий граф для данного
предложения
|
|
Набор объектных функций, рассмотренный в данной статье, не является исчерпывающим и
демонстрирует только основные идеи реконфигурации регулярных сетей.
Литература
1. Дорогов А. Ю. Структурный синтез модульных
слабосвязанных нейронных сетей. Часть 2
Ядерные нейронные сети // Кибернетика и системный анализ. 2001.-№4.-с.13-20
2. Дорогов А. Ю. Порождающие грамматики регулярных
модульных нейронных сетей // Труды 8-й Всероссийской конференции “Нейрокомпьютеры
и их применение” НКП-2002. Москва 21-22 марта 2002г. с. 944-954.