Актуальной задачей превентивной медицины является неинвазивное измерение содержания глюкозы в крови человека. Принцип измерения основан на определении косвенных признаков, – параметров термочувствительности в тесте Акабане, которые сложным образом связанны с содержанием глюкозы. Зависимость является индивидуальным свойством организма и должна определяться для каждого человека отдельно. Метод измерения включает непосредственное измерение параметров термочувствительности и последующее вычисление содержания глюкозы по разработанному алгоритму. Алгоритм измерения включает модель механизма поддержания уровня глюкозы в крови человека, отражающую связь содержания глюкозы и термочувствительности.
Модель механизма поддержания глюкозы в крови человека
может быть представлена как нелинейная динамическая система, параметры которой
подлежат оцениванию при градуировке алгоритма. Для имитации модели применяется
рекуррентная нейронная сеть (НС). НС представляет собой адаптивную систему, моделирование
которой не требует предварительного расчета параметров (рис.1).
Первоначальное оценивание параметров модели
выполняется в процессе обучения НС. В дальнейшем в процессе эксплуатации по
мере поступления дополнительных данных выполняется подстройка параметров модели
в результате выполнения процедуры адаптации.
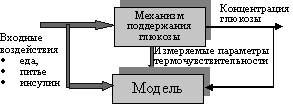
Рис.1
Моделирование механизма поддержания глюкозы
Метод измерения, построенный на основе НС, может быть
отнесен к методам интеллектуальных измерений,
поскольку он основан на знаниях, получаемых о каждом пациенте, путем оценивания
индивидуальных параметров модели. Метод позволяет расширять первоначально
полученные знания путем уточнения параметров модели в процессе эксплуатации
измерительной системы и при адаптации алгоритма, а затем использовать
заключенную в параметрах модели информацию для восстановления концентрации
глюкозы, содержащейся в теле испытуемого.
Для повышения устойчивости результатов измерения кроме
измеренных параметров термочувствительности на вход НС подаются данные о фактах
“событий” приема пищи и введения инсулина. В информационных массивах эти
события представлены в виде импульсов, появляющихся в момент приема пищи или инсулина.
Амплитуды импульсов пропорциональны количеству принятой пищи или количеству
инсулина. При этом в процессе обучения сети решаются одновременно две задачи:
обучение правильному представлению во времени предикторов, связанных с приемом
пищи и инсулина, и обучение определению содержания глюкозы на основе входных
предикторов.
Важным этапом разработки алгоритма является выбор
архитектуры НС. Сеть должна представлять
адекватную модель поддержания глюкозы в крови человека, поэтому, как показали
исследования, она должна иметь достаточно высокую размерность. Объем
экспериментальных данных, используемых в процессе обучения НС, должен быть
достаточным для правильного обучения, однако выполнение масштабных экспериментов
при градуировке сети большой размерности практически трудно выполнимо. Поэтому
объем экспериментальных данных является важным ограничением, приводящим к
необходимости уменьшения размера сети и обеспечения устойчивости за счет
упрощения архитектуры. Выбор архитектуры нейронной сети зависит от числа слоев и
числа нейронов в каждом слое, типа активационных функций нейронов, числа задержек
в блоке задержек и вида обратных связей.
Использована сеть с логистической активационной
функцией нейронов в скрытых слоях и линейной активационной функцией в выходном
слое. Наличие 400-600 испытаний, доступных для градуировки алгоритма, и
требование обеспечения 10%-ной погрешности
результата, позволяет заключить, что сеть может иметь не более 40-60 свободных
параметров.
Использована архитектура нелинейной авторегрессионной
модели сети с внешними входами, - NARX модель (Nonlinear autoregressive with exogenous inputs), представленная
на рис. 2. Выходы сети 
зависят от 
, трактуемого в терминах модели пространства состояний, и от входных
векторов 
:
где q - размерность пространства состояний. Уравнение
наблюдения динамической нейронной сети имеет вид:
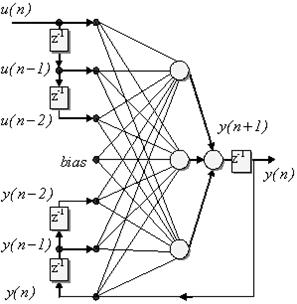
Рис.2
NARX нейронная сеть с тремя скрытыми нейронами
Объединение этих уравнений, приводит к следующей
зависимости:
Используя определения 
и , позволяет преобразовать (3) в форме:
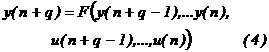
Замены индекса времени 
на 
преобразует (4) в
выражение (5):
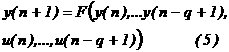
Выход НС 
определяется как
нелинейное преобразование F от текущих и задержанных входных параметров 
, а также от предыдущих значений выходного параметра 
. В этом случае модель пространства состояний является наблюдаемой.
NARX модель с общей обратной связью, поступающей с
выходного нейрона, способна имитировать полную рекуррентную архитектуру сети,
описание которой соответствует модели пространства состояний.
Предложенная НС имеет три слоя нейронов и блок
задержек входных сигналов длиной q=3 и такой же
блок задержки выходных сигналов. Сеть, применявшаяся расчетах для более чем
сорока пациентов, имеет размер 26-3-3-1. Число коэффициентов несколько велико
для оценки по данным, доступным для обучения, поэтому в отдельных случаях
выполнялось снижение размерности сети.
Для снятия избыточности, связанной с небольшой
взаимной коррелированностью параметров, выполнялось преобразование декорреляции
(Карунена-Лоэва). При переходе к
некоррелированным предикторам использован критерий сохранения не менее
99% энергии исходных входных предикторов. Как показало исследование, декоррелирующее
преобразование позволило сократить количество весов сети до приемлемого
значения. Общее их количество варьирует от 40 до 60 и зависит от индивидуальных
различий исследованных пациентов. При предварительной обработке динамики значений глюкозы, полученных инвазивным
методом и предназначенных для обучения сети, выполнялось восстановление
значений глюкозы на тех интервалах, где измерения не выполнялись, и сглаживание
измеренных значений глюкозы для уменьшения случайных погрешностей измерения.
Использован метод восстановления кубическими сплайнами по условию минимума
среднего квадрата ошибки. Этот метод позволил восстановить значения глюкозы на
интервалах, где измерения отсутствовали, и уменьшить случайную погрешность
измерения.
Обучение НС важно проводить так, чтобы равномерно
учитывать все экспериментальные данные. Особое значение это имеет при адаптации
алгоритма в процессе эксплуатации измерительной системы. При обучении в
реальном времени обычно используется так называемое непрерывное обучение,
реализуемое по алгоритму, основанному на градиентном спуске. Недостаточное
качество обучения этим методом связано с тем, что алгоритм использует
мгновенные оценки градиентов. Это серьезное ограничение преодолевается при трактовке
обучения с учителем как задачи оптимальной фильтрации. Такая форма алгоритмов
рекурсивно использует информацию, содержащуюся в обучающих данных, как бы
обращаясь обратно к первой итерации процесса обучения. Суть концепции лучшим
образом отражена в теории фильтров Калмана. Поэтому в наших исследованиях
использован метод обучения НС с помощью алгоритма на основе фильтра Калмана.
Метод и алгоритм позволяют
·
Применить теорию
моделей пространства состояний, в которых эффективно используется информация,
содержащаяся в исходных данных;
·
Оценивать
состояния модели рекурсивно так, что каждая следующая оценка вычисляется из
предыдущей оценки и только последняя подлежит хранению.
Измеренные значения параметров термочувствительности
иногда содержат аномальные значения, наличие которых может существенно ухудшить
работу алгоритма и которые приходится удалять из состава данных. Под
аномальными фрагментами результата
измерения понимаются отсчеты, поступающие с измерительной системы через канал
связи в ЭВМ и содержащие погрешность, в несколько раз превышающую по величине
нормальную погрешность измерения, распределение которой полагается
удовлетворяющей закону Гаусса.
Пакеты сильно коррелированных аномальных результатов
измерения обусловлены кратковременными групповыми сбоями в измерительной
аппаратуре и в каналах связи. Иногда пакеты содержат целую группу из нескольких
аномальных результатов измерения, значения которых достаточно сильно
коррелированы.
Измерения входных
параметров выполняются с постоянным шагом дискретизации. Однако в процессе
выполнения измерений или при передаче по каналу связи встречаются случаи потери
данных. Связанные с этим пропуски данных приводят к неравномерности отсчетов в
выборки, что делает ее непригодной для использования в нейросетевом алгоритме.
Поэтому на этапе предварительной обработки данных выполняется восстановление
потерянных интервалов выборки, если длина их не слишком велика. С этой целью,
на этапе предварительной обработки с помощью разнообразных методов интерполяции
и фильтрации выполняются
· Восстановление отдельных единичных аномальных
результатов измерения;
· Процедуры восстановления пакетов коррелированных
аномальных отсчетов измерения;
· Восстановление потерянных пакетов, содержащих
результаты измерения.
Чтобы уменьшить неопределенность измерения глюкозы,
связанную с различными вариантами начальной инициализации сети, выполняется
осреднение результатов восстановления по нескольким калибровкам сети. В
процессе калибровки обучаются девять
сетей с одинаковой структурой. Ошибки обучения запоминаются в отдельном файле.
Восстановление выполняется по трем нейронным сетям,
имеющим лучший результат обучения. При этом восстановленное значение
определяется соотношением: 
где 
- результат
восстановления глюкозы по k-ой обученной
НС.
Предложенная система неинвазивного косвенного
измерение содержания глюкозы в крови человека позволяет выполнять измерения с
достаточно большой точностью. Тестирование системы производилось на наборах
экспериментальных данных для больных диабетом различных типов, а также для
здоровых людей. Максимальная ошибка восстановления составила 5-15% для здоровых
пациентов, и 10-45% для больных диабетом первого типа. При этом некоторые
наборы экспериментальных данных не позволяли осуществлять адекватное
моделирование, и, соответственно, производить измерения. В настоящий момент ведутся
исследования с целью повышения точности предсказания, а также разрабатываются
более совершенные методы адаптивной фильтрации для снижения погрешности входных
сигналов.
Литература
1.
Haykin S. Neural networks. A comprehensive foundation
/ Upper Saddle River (New Jersey): Prentice Hall, 1999. – 842 p.
2.
Химмельблау Р. Прикладное нелинейное программирование, М: Мир, 1975. –
492c.
3.
Singhal S., Wu, L. Training
Multilayer Perceptrons with the Extended Kalman Algorithm – Advances in Neural
Information Processing Systems, 1, 133-140, 1989.
4.
Williams, R.J. Some
Observations on the Use of the Extended Kalman Filter as a Recurrent Network
Learning Algorithm – Colleage of Computer Science, Northeastern University,
Boston, TR NU-CCS-92-1, 1992.
5.
Puskorius, G.V., Feldkamp,
6.
Lange, F. Fast and Accurate
Training of Multilayer Perceptrons Using an Extended Kalman Filter (EKFNet) –
Institute for Robotics and Systems Dynamics, Wessling, internal paper, 1995.
7.
De Schutter, J., De Geeter,
J., Lefebvre, T, Bruyninckx, H. Kalman Filters: A Tutorial – 1999.
8.
Welsh, G., Bishop, G. An
Introduction to the Kalman Filter - Department of Computer Science, University
of North Carolina, TR 95-041, 2002.
9.
Leleux, D.P., Claps, R.,
Chen, W., Tittel, F.K., Harman, T.L, Applications of Kalman filtering to
real-time trace gas concentration measurements – Applied Physcis B 74, pp.
85-93, 2002.
10.
Werbos, D. Backpropagation
through time – Proceedings of the IEEE, vol. 78, No. 10, 1550-1560, 1990.