Нейронные сети являются мощным инструментом решения различных задач обработки информации. Разработаны различные архитектуры сетей, отвечающие самым разнообразным требованиям. Возможно, наибольшее распространение получила архитектура сети «многослойный персептрон» ([1]).
Важнейшим фактором, определяющим качество работы сети, является выбор алгоритма ее обучения. Классическим алгоритмом обучения является алгоритм обратного распространения ([1]). Он получил широкое распространение в силу своей простоты. Данный алгоритм не всегда способен обеспечить адекватное качество обучения. Разработаны более совершенные методы, из них наиболее перспективным в данный момент считается алгоритм обучения, основанный на теории фильтров Калмана ([2,3]).
В данной работе проводится сравнительный анализ этих двух алгоритмов обучения на примере задачи предсказания сигнала.
Алгоритм
обратного распространения
Алгоритм обратного распространения ([1])
является методом градиентного спуска, предназначенным для настройки весов в
многослойной сети. Для обучения требуется множество обучающих векторов 
, каждому из которых соответствует вектор желаемого отклика
сети 
. Процесс обратного распространения состоит из двух фаз:
прямой и обратной. В течение прямой фазы на вход сети подается вектор , и сеть генерирует выходной сигнал 
. В ходе обратной фазы осуществляется настройка весов сети на
основании вычисленной ошибки:
(1)
где 
- значение ошибки, 
- выходной вектор сети
и 
- вектор желаемого
отклика сети.
Веса сети изменяются таким образом, чтобы приблизить действительный отклик сети к желаемому отклику:
(2)
(3)
где 
- значение некоторого
весового коэффициента сети для момента времени 
, 
- параметр, задающий
скорость обучения.
Благодаря своей простоте, алгоритм обратного распространения обладает большой скоростью работы. В практических применениях обучение состоит в последовательном представлении сети векторов из некоторого обучающего множества. Полное представление всех векторов множества называется эпохой. Изменение весов может осуществляться после представления каждого вектора, или после представления нескольких векторов из выборки (обучение эпохами). Обучение эпохами является более качественным, улучшение в первом случае можно добиться, меняя порядок представления векторов.
Алгоритм, основанный на фильтре Калмана
Алгоритм обратного распространения, являясь методом градиентного спуска, обладает всеми недостатками подобного рода методов. Большинство из них позволяет решить калмановский алгоритм обучения ([4]).
Впервые возможность применения теории фильтров Калмана к задаче обучения многослойного персептрона была продемонстрирована Singhal и Wu ([5]).
Фильтр Калмана позволяет оценивать состояние объекта, который может моделироваться как линейная система, управляемая аддитивным белым шумом, при этом доступные измерения являются линейной комбинацией вектора состояния с добавлением белого шума ([6,7,8]).
Применение теории калмановских фильтров для нелинейных систем обеспечивается линеаризацией. Полученный подобным образом фильтр Калмана называется расширенным ([6]).
При обучении нейронной сети с помощью фильтра Калмана считается, что нейронная сеть представляет собой нелинейную динамическую систему, состояние которой задается значениями всего множества весовых коэффициентов. Значения, измеряемые фильтром, принимаются равными желаемому отклику сети:
(4)
(5)
где 
- вектор состояния,
содержащий все весовые коэффициенты сети, 
- входной вектор сети
из обучающего множества, 
- соответствующий
выходной вектор, 
- нелинейная функция, 
- шум процесса в
модели системы, а 
- шум измерения.
Калмановский фильтр является рекурсивным алгоритмом, состоящим из следующих шагов ([7]):
1
Выбор начальных оценок 
и 
.
2
Линеаризация:
3
Вычисление коэффициента усиления Калмана: 
, 
4
Коррекция текущей оценки: 
.
5
Коррекция оценки дисперсии ошибки: 
.
6
Предсказание величины: 
.
7
Предсказание дисперсии: 
.
8 Переход на шаг 2, (6)
где 
- априорная оценка
состояния системы для шага , 
- апостериорная оценка
состояния, 
- априорная оценка
ковариационной матрицы, 
- апостериорная
оценка, 
- коэффициент усиления
Калмана, 
- функция
преобразования нейронной сети, 
- ее линеаризованная
форма, 
- вектор измерения, - шум процесса и - шум измерения.
Линеаризация требует вычисления производных от функции преобразования нейронной сети. Для вычисления обычно используется алгоритм обратного распространения сквозь время ([9]) или алгоритм темпорального обратного распространения ([10]).
Из соображений оптимизации часто применяется
расщепленная расширенная версия фильтра Калмана. За счет игнорирования взаимодействия
между определенными группами весов матрица ковариации 
приводится в
блочно-диагональной форме, что снижает вычислительные затраты ([1]). Данная
оптимизация также ухудшает качество обучения. Современные настольные компьютеры
позволяют для большинства приложений использовать нерасщепленную
версия алгоритма.
Условия
эксперимента
Для сравнения качества обучения сети с использованием алгоритма обратного распространения и калмановского алгоритма использовалась задача предсказания сигнала. В качестве входных данных были выбраны два сигнала: простой синусоидальный сигнал, а также сигнал, полученный с помощью уравнения Маки-Гласса ([11]). Задачей являлось автономное предсказание на временном интервале, составляющем 10% от интервала обучения.
В обоих случаях использовалась одна и та же архитектура сети – многослойный персептрон с задержками на входе. Данная архитектура представляет собой простейшую форму темпоральной нейронной сети ([12]). Длина линии задержки составляла 16 временных отсчетов.
Обучение осуществлялось до достижения заданного порога среднеквадратичной ошибки, составляющего 0,01. Далее выполнялось тестирование, заключавшееся в предсказании сигнала в автономном режиме. Автономный режим предсказания использует предсказанное на предыдущем шаге значение сигнала в качестве входного значения на следующем шаге.
Таблица 1 содержит значения ошибок обучения и тестирования, а также время обучения, для различных сигналов и типов алгоритма.
Таблица 1
|
Сигнал |
Алгоритм обучения |
Ошибка предсказания |
Количечтво эпох / время обучения |
|
Синус |
Обратное распространение |
0,012 |
285 / 2 с. |
|
Маки-Гласс |
Обратное распространение |
0,015 |
300 / 3 c. |
|
Синус |
Расширенный фильтр Калмана |
0,001 |
9 / 1 с. |
|
Маки-Гласс |
Расширенный фильтр Калмана |
0,002 |
85 / 9 с. |
Результаты предсказания сигнала Маки-Гласса для двух алгоритмов обучения представлены на следующих рисунках.
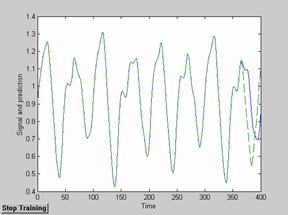
Рисунок 1. Результат предсказания сигнала Маки-Гласса для сети, обученной алгоритмом обратного распространения
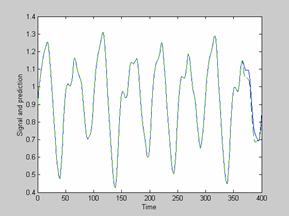
Рисунок 2. Результат предсказания сигнала Маки-Гласса для сети, обученной калмановским алгоритмом
Из приведенных экспериментальных данных видно, что алгоритм обучения, основанный на расширенном фильтре Калмана, значительно превосходит алгоритм обратного распространения по скорости сходимости (количество эпох) и точности предсказания. Единственным недостатком является несколько увеличенное время обучения.
Заключение
Применение алгоритма обучения нейронной сети, основанного на теории фильтров Калмана, позволяет значительно улучшить качество обучения, сократив при этом количество обучающих эпох. Для рассмотренных примеров предсказания сигнала ошибка при восстановлении сигнала калмановской сетью была почти на порядок ниже ошибки, полученной для «обычной» сети, использующей алгоритм обратного распространения.
Недостатком калмановского алгоритма является увеличение вычислительных затрат. Производительность современных настольных компьютеров такова, что данный недостаток в большинстве случаев несущественен.
Системы, построенные на базе калмановских сетей, позволяют адекватно моделировать объекты различной степени сложности, обеспечивают устойчивость к ошибкам во входных данных и обладают улучшенной обобщающей способностью.
Литература
1.
Haykin, S. Neural Networks,
A Comprehensive Foundation, 2nd edition, Macmillan, 1999.
2.
Williams, R.J. Some Observations
on the Use of the Extended Kalman Filter as a Recurrent Network Learning
Algorithm – Colleage of Computer Science, Northeastern University, Boston, TR
NU-CCS-92-1, 1992.
3.
Lange, F. Fast and Accurate
Training of Multilayer Perceptrons Using an Extended Kalman Filter (EKFNet) –
Institute for Robotics and Systems Dynamics, Wessling, internal paper, 1995.
4.
Puskorius, G.V., Feldkamp,
5.
Singhal S., Wu, L. Training
Multilayer Perceptrons with the Extended Kalman Algorithm – Advances in Neural
Information Processing Systems, 1, 133-140, 1989.
6.
Welsh, G., Bishop, G. An
Introduction to the Kalman Filter - Department of Computer Science, University
of North Carolina, TR 95-041, 2002.
7.
De Schutter, J., De Geeter,
J., Lefebvre, T, Bruyninckx, H. Kalman Filters: A Tutorial – 1999.
8.
Leleux, D.P., Claps, R.,
Chen, W., Tittel, F.K., Harman, T.L, Applications of Kalman filtering to
real-time trace gas concentration measurements – Applied Physcis B 74, pp.
85-93, 2002.
9.
Werbos, D. Backpropagation
through time – Proceedings of the IEEE, vol. 78, No. 10, 1550-1560, 1990.
10. Chappelier J., Gori M., and Grumbach A. Time in Connectionist Models. In: Sequence Learning:
Paradigms, Algorithms and Applications,
Springer, 2001.pp. 105-134.
11.
Day, S. and
12.
Waibel, A., Hanazava, T.,
Hinton, G., Shikano, K., Lang, K., Phoneme recognition using time-delay neural
networks, IEEE trans. on Signal Processing, 37(3), pp. 328-339, 1989.