Аппарат нейронных сетей доказал свою эффективность во многих задачах
анализа данных, в которых трудно или невозможно построить адекватную
аналитическую модель. Нейронные сети позволяют найти скрытые зависимости в
числовых данных, которые могут иметь большой объем и быть сильно зашумлены.
В настоящее время нейросетевая технология является одной
из наиболее динамично развивающихся областей искусственного интеллекта и
успешно применяется в различных прикладных областях, таких как:
1. Прогнозирование различных экономических
показателей (курсов валют и акций, кредитных и иных рисков и др.).
2. Биомедицинские приложения (диагностика
различных заболеваний, идентификация личности).
3. Сложные системы управления.
4. Распознавание образов.
5. Геология (прогнозирование наличия полезных
ископаемых).
6. Экология и науки об окружающей среде (прогнозы
погоды и различных катаклизмов).
7. Игры.
В математической физике имеется достаточно широкий
круг задач, многие из которых решены аналитически, а к исследованию остальных
найдены различные численные подходы. Однако это не мешает рассматривать
использование нейронных сетей в качестве новой методологии решения как старых,
так и новых задач.
Рассмотрим, к примеру, задачу Дирихле для
круга 
Известно, что её решение представляется интегралом Пуассона
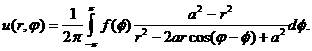
Вычислить аналитически этот интеграл можно только
в исключительных случаях, поэтому его, как правило, приходится находить численно.
С другой стороны, для решения этой задачи можно
применить какой-либо численный метод – сеток, конечных элементов, Галёркина и
т.п. Последние два заключаются в поиске приближённого решения в виде
где 
- изначально заданные функции.
Далее минимизируется некоторый функционал ошибки –
для задачи Дирихле это
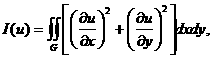
если не считать слагаемого, связанного с граничным условием. Это слагаемое
записывается очевидным образом для каждого рода граничных условий. Минимизация
функционала 
позволяет определить
коэффициенты 
, при этом структура функций в методе конечных элементов
подбирается таким образом, чтобы матрица получающейся системы линейных
уравнений содержала больше нулей.
Эта конструкция очень напоминает один из видов
нейронных сетей – RBF (сети с радиальными базисными функциями). Для этих сетей 
, где 
- текущая точка, а 
- некий набор точек плоскости. При этом метод
конечных элементов получается как частный случай RBF–сети при соответствующем выборе функции
и нормы 
. В качестве функции 
обычно берут Гауссов пакет 
или функцию Коши 
.
Парадигма нейронных сетей позволяет подойти к
этому вопросу по-другому. Во-первых, в процессе обучения (минимизации ) помимо можно изменять 
, 
и даже
само выражение нормы, задавая её некоторой квадратичной формой (или положительно
определенной функцией), коэффициенты которой тоже изменяются в соответствии с
выбранным алгоритмом обучения. Во-вторых, помимо функционала можно найти непосредственно
и минимизировать 
, вычисляя лапласиан аналитически.
Подобно тому, как это сделано в [2], можно искать
решение в виде двух слагаемых – одно удовлетворяет граничному условию и не
содержит подбираемых параметров, а другое – уравнению с учётом первого
слагаемого и содержит подбираемые параметры. Этот прием подходит только для
линейных задач.
Вместо RBF можно использовать и другие нейросетевые модели,
например многослойный персептрон.
Этот вид сети является наиболее употребительным и
исследованным. Опишем его подробнее. На вход сети подается m-мерный вектор x.
Линейные комбинации координат входа поступают на вход первого слоя нейронов (коэффициенты
этих комбинаций будем называть весами первого слоя). Каждый нейрон представляет
собой нелинейную функцию, которая называется функцией активации. Линейные
комбинации выходов нейронов подаются на следующий слой, а линейные комбинации выходов
нейронов последнего слоя образуют выход сети. Выбор архитектуры сети, то есть
числа слоев, количества нейронов в каждом слое является нетривиальной задачей,
которую в данной работе мы оставляем в стороне. При этом наиболее
перспективными представляются такие алгоритмы обучения, согласно которым
подбирается и архитектура сети, а не только ее веса.
Для сингулярных задач можно использовать
гетерогенные сети, в которых часть нейронов имеет два входа 
и
и функцию активации 
, а часть – функцию активации 
. Класс таких моделей включает в себя и аппроксимации Паде.
Можно использовать принципиально другой подход:
вычислить решение с помощью интеграла Пуассона в достаточно представительном
наборе точек, а потом проинтерполировать на всю область с помощью нейронной
сети.
Интересное обобщение описанного выше нейросетевого
подхода к решению задачи Дирихле получается, если в качестве входов сети использовать
не только x и y (или 
и 
), но и граничные значения 
в некотором наборе
точек. Обученная таким образом нейронная сеть позволяет получить решение задачи
Дирихле не при фиксированных, а при произвольных граничных условиях (функция f задаётся таблично в этом наборе точек).
Аналогично можно поставить и решить обратные
задачи разного рода – например, определить граничные условия по решению,
задаваемому в некотором наборе точек. Делается это следующим образом:
1)
Находится
решение в заданном множестве точек круга при различных граничных
условиях 
. Таким образом создается набор данных для обучения сети,
причем этот набор должен быть достаточно представительным.
2)
Обучается
сеть (или набор сетей), выходом которой являются граничные условия в указанном
наборе точек (граничное условие в фиксированной точке). Обучение осуществляется
на основе минимизации некоторого функционала (например, сумме квадратов
отклонений выходов сети от упомянутых в п.1 предписанных значений).
3)
Обученная
сеть может выдавать граничные условия по требуемым значениям
решения в заданном множестве внутри круга.
Вместо решения в наборе точек можно использовать и
другие условия – минимум некоторого вспомогательного функционала, ограничение
решения некоторыми дополнительными условиями и т.п.
Если решение на части границы известно, то
соответствующие значения можно включить в число входов сети, оставив в качестве
выходов значения в точках оставшейся
части границы.
Очевидно, что методология применения нейронных
сетей слабо зависит как от уравнения, так и от формы области и типа граничных
условий. Уравнение и граничные условия могут быть и нелинейными, достаточно
сопоставить им минимизируемый функционал типа . Если область имеет особенности, например, острые углы, в их
окрестности можно взять больше точек (как при аппроксимации интегралов вида , так и при интерполяции ).
Аналогично ставятся и решаются комбинированные задачи,
когда рассматриваемое уравнение в разных подобластях имеет разный вид. Более
того, переменной, подлежащей определению, можно считать и саму форму области. При
этом границу можно задавать некоторым набором
точек или рассматривать как элемент некоторого параметрического
семейства, параметры которого подлежат определению.
Рассмотрим для примера следующую модельную
постановку задачи: пусть 
- гладкое семейство областей в 
, зависящее от некоторого параметра 
(который может быть и
векторным); 
- эллиптический оператор, 
- допустимый граничный оператор, 
- комплексное число. С множеством решений семейства краевых
задач
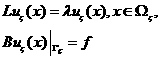
свяжем следующую экстремальную задачу: требуется найти область
из заданного семейства, доставляющую некоторому функционалу 
экстремальное значение.
Один из возможных классических методов решения такой экстремальной задачи с
условием связи в дифференциальной форме состоит в ее замене необходимым
условием экстремума 
с условием связи в виде
граничного интегрального уравнения, получаемого из краевой задачи прямым
методом [4].
К подобной задаче приводит, например, построение
математических моделей поверочных установок и прецизионных датчиков переменного
давления, связанное с изучением в линейном приближении гармонических по времени
акустических колебаний. На известной части границы ставится третье краевое
условие, на неизвестной, подлежащей определению части 
– однородное условие
Неймана. Вид функционала 
определяется
требованиями, предъявляемыми к акустическому волновому полю на датчике,
помещаемом, как правило, на подбираемой неизвестной границе : это может быть и точечный функционал вида 
и функционал вида
где интегрирование ведется по области, занятой датчиком.
Указанный классический прямой метод приводит к алгоритму итерационного типа:
заданное приближение 
для позволяет найти
предельные значения решения на границе 
(а тем самым и внутри
области), а затем корректировать границу при помощи уравнения Эйлера и, таким
образом, определить 
. При этом начальное приближение 
выбирается обычно из
физических соображений.
Методология нейронных сетей позволяет не только
переформулировать постановку задачи в нейросетевом базисе, но и рассмотреть
случаи нелинейных моделей. Самый простой
вариант – искать 
как нейросетевую
функцию своих аргументов, подбирая веса
сети так, чтобы получалось решение краевой задачи, и далее находить из условия экстремума
J . При этом для каждых и строится своя сеть. Далее можно строить сеть,
у которой входами будут и значения в некотором фиксированном наборе точек, а выходом
- . При этом надо будет набрать исходную базу данных, т. е.
решить задачу для достаточно представительного набора параметров. Оба этапа
совместимы с помощью одной гетерогенной сети. Очевидно, что нелинейность
практически не усложняет задачу.
Аналогично решаются задачи восстановления
уравнения (или граничного условия) как элемента некоторого параметризованного
семейства. Нейросетевой подход к решению обратных задач такого рода может
рассматриваться как один из методов их регуляризации.
Можно поставить и более экзотические задачи. Например,
ищется функция, которая в некоторой области
(или ее части) определяется не уравнением, а некоторым экспериментальным материалом
и, возможно, некоторыми законами сохранения. Еще одну группу образуют задачи
моделирования физических процессов с фазовыми переходами. Разумность применения
нейросетевых методов к ним связана с тем, что типичная функция активации в многослойном персептроне имеет ступенчатый вид.
Мы оставляем в стороне некоторые другие задачи и
подходы, за которыми отсылаем читателя к [2], [3] и [5].