Алгоритмы
геофизической интерпретации данных геофизических исследований скважин
используют решение прямой задачи, определяющей зависимости измеряемых
геофизических параметров от изучаемых характеристик разреза [1]. Интерпретация
данных комплекса геофизических исследований скважин относится к классу особо
сложных задач, решаемых в условиях неполной информации. В большинстве существующих
методик комплексной интерпретации не заложен принцип адаптивности, т.е.
самонастройки к условиям измерений. Этот фактор оказывает негативное влияние на
качество и скорость интерпретации данных.
В известных системах обработки геофизической информации интерпретация геофизических параметров проводится либо в попластовом, либо в поточечном варианте [1,2]. При попластовой интерпретации непрерывная кривая зависимости геофизических параметров от глубины заменяется ступенчатой. Каждая ступенька соответствует некоторому геометрическому объекту (пласту). Пласт характеризуется осредненными геофизическими свойствами. Основная проблема при данном методе интерпретации заключается в неоднозначном разбиении геофизической кривой на пласты. При поточечной интерпретации проводится обработка оцифрованной зависимости геофизических параметров от глубины разреза. Результатом обработки является зависимость характеристик разреза от его глубины. Решение задачи поточечной интерпретации основано на методах обратной фильтрации, учитывающих влияние пород, окружающих исследуемую точку. Основной проблемой применения метода поточечной интерпретации является значительная вычислительная трудоемкость. Возможности повышения эффективности поточечной интерпретации связаны с применением алгоритмов, относящихся к «интеллектуальным алгоритмам» [3].
Обозначим
свойства разреза вектором 
. В качестве таких свойств обычно выступают: коэффициент
пористости 
, коэффициент глинистости 
, коэффициент водонасыщенности 
, коэффициент нефтенасыщенности 
и т.д. Для
проведения геофизических исследований скважин применяются несколько методов:
электрометрические, акустические, радиометрические, термометрические и др. Для
каждого метода имеется регистрируемый сигнал 
, определяющий физические характеристики (электрическое сопротивление,
скорость распространения звуковой волны,
уровень радиоактивного излучения), связанные со свойствами разреза. Эта связь
может быть задана в виде петрофизических уравнений:
Y = F(X) (1)
Существующие
геофизические методы не являются точечными [4]. При измерении физической характеристики
в точке 
в цилиндрической
системе координат (r,z), где z – расстояние по оси скважины, r – радиус,
отсчитываемый от оси, на величину регистрируемого сигнала оказывают
характеристики окружающего пространства, а также аппаратурные погрешности. В
результате регистрируемый сигнал определяется выражением вида
(2)
Учет радиальной составляющей требует численного решения сложных многомерных дифференциальных эллиптических уравнений. Поэтому в уравнении (2) при практической реализации оставляют только осевую неоднородность
(3)
При интерпретации результатов геофизических исследований необходимо восстановить вектор свойств разреза X(z) по зарегистрированным значениям физических характеристик Y(z) на основе модели взаимодействия (3).
Наиболее часто в автоматизированных системах интерпретации используются следующие петрофизические уравнения вида Y = F(X):
,
,
,
,
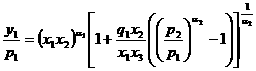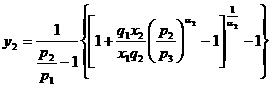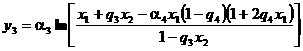
(4)
где
векторы 
, 
соответствуют свойствам разреза и регистрируемым сигналам;
векторы 
, 
описывают общие
физические свойства пород; 
– вектор эмпирических
коэффициентов.
Уравнения (4) соответствуют записи
Y = (X, P, Q, a). (5)
Если поточечная интерпретация проводится без учета осевой
неоднородности, то для нахождения свойств разреза 
по показаниям геофизических методов 
используется система уравнений (5). Определение
X сводится к задаче нелинейного программирования.
Определяется критерий оптимизации и составляется целевая функция
(6)
где
K –
количество точек в направлении z;
– метрика; 
– нормированный вектор весовых коэффициентов.
К целевой функции добавляются
ограничения, задающие область определения
. (7)
Задачу условной оптимизации можно привести к эквивалентной задаче
безусловной оптимизации параметрическим методом штрафных функций
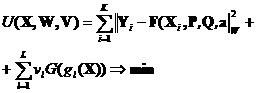(8)
где
- параметрический
вектор; 
- функционал,
обеспечивающий условие 
.
При K = 1 свойства X определяются в рассматриваемой точке при известных
параметрах 
. Если обозначить 
- вектор неизвестных
параметров, то вместо (8) запишем
(9)
Для решения задачи (9) целесообразно применить генетический алгоритм,
являющийся разновидностью прямых методов оптимизации. Данный алгоритм подробно
описан во многих литературных источниках [5]. Алгоритм относится к классу
интеллектуальных алгоритмов и основан на представлении вектора S в виде закодированной хромосомы. Эффективность
данного алгоритма проверялась при решении вариационных задач при оптимальном
управлении динамическими системами [6].
Вид сигналов Y(z) свидетельствует о наличии осевой неоднородности, как
это видно на рис. 1.
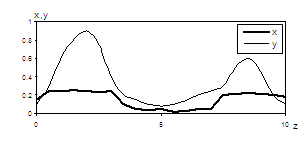
Рис.
1. Зависимость свойства разреза и геофизического сигнала от глубины скважины
Для более точного восстановления свойств разреза X необходимо
использовать выражение (3). В качестве функции осевого влияния возьмем функцию
Гаусса
.
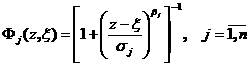При известных параметрах 
задача восстановления
свойств X также сводится к задаче (9).
При решении задачи (9) предполагалось, что коэффициенты (P,Q,a) в
уравнениях (4) известны. Для их определения необходимо иметь обучающую выборку 
. При наличии данных о коэффициентах P,Q,
характеризующих общие свойства пород, проводится настройка коэффициентов a,W. Для обучения
могут привлекаться данные разных месторождений и с нескольких скважин, т.е. 
. Настройка коэффициентов производится при решении следующей
задачи безусловной оптимизации:
(10)
После вычисления коэффициенты a,W могут применяться в процессе поточечной интерпретации
для произвольных месторождений.
При
отсутствии данных о коэффициентах P,Q подбор этих коэффициентов производится на основе
обучающих данных, полученных на конкретном месторождении
(11)
Подобранные таким образом коэффициенты (a,P,Q,W) могут применяться при интерпретации геофизических
данных рассматриваемого месторождения.
Задачи настройки коэффициентов (10),(11) являются разовыми и не
предъявляют повышенных требований к алгоритмам оптимизации. При проведении
поточечной обработки кривых геофизических методов оптимизационная задача (9)
должна решаться многократно, в каждой точке разреза. Более эффективным, с точки
зрения минимума вычислительных затрат, является применение алгоритма,
основанного на нейронных сетях [7]. Обозначим
(12)
алгоритм,
реализующий однонаправленную сеть на основе многослойного персептрона: 
- входной вектор; 
- выходной вектор; 
, 
,
,
.
Обучение сети (12), т.е. определение синаптических коэффициентов W,
проводится на обучающей выборке 
. Выборка может быть получена генерацией данных по алгоритму
(3),(4) при известных параметрах (P,Q,a), либо составлена из имеющихся данных геофизических
исследований. Входной вектор xi,
соответствующий i-й точке, формируется из показаний геофизических
методов в окне шириной 
, 
- интервал между
точками измерения, 
.
Выходной вектор соответствует свойствам разреза 
. Введение окна 
позволяет учитывать
осевую неоднородность разреза.
Область применения обученной сети (12) определяется
составом обучающей выборки.
Для моделирования процесса интерпретации были
сгенерированы данные Y(z) для заданных свойств разреза X(z) по
уравнениям (3),(4). Фрагмент зависимости Y(z) для четырех методов показан на рис. 2. Затем на
половине этих данных (
, 
) проведено обучение нейронной сети (12) и свойства X(z)
восстановлены на другой половине данных.
Рис. 2. Данные геофизических
методов по глубине
На рис. 3 представлены восстановленные и исходные значения свойств
разреза. Как следует из рис.
3, восстановленные зависимости отслеживают
заданные (фактические) значения X(z). По восстановленным зависимостям уверенно
производится разбиение разреза на пласты и
определяются литологические свойства. Обученная таким образом сеть готова к
оперативной интерпретации геофизических данных.
Рис. 3. Восстановленный нейронной сетью
коэффициент общей пористости
Литература
1.
Дьяконова Т.Ф. Применение ЭВМ при интерпретации данных геофизических
исследований скважин. – М.: Недра, 1991. – 220 с.
2.
Обработка и интерпретация данных промысловых геофизических исследований
на ЭВМ: Справочник/ Н.Н.Сохранов, С.М.Аксельрод, С.М.Зунделевич, И.М.Чуринова.
– М.: Недра, 1989. – 240 с.
3.
Тененев В.А., Сенилов М.А., Паклин Н.Б. Определение продуктивных
коллекторов с помощью обучающихся информационных систем. // Вестник ИжГТУ. –
Ижевск: Изд-во ИжГТУ, 2002. – Вып. 5. – С. 31-34.
4.
Латышова М.Г., Вендельштейн Б.Ю., Тузов В.П. Обработка и интерпретация
материалов геофизических исследований скважин. – М.: Недра, 1990. – 308 с.
5.
Курейчик В.М., Зинченко Л.А., Хабарова И.В. Алгоритмы эволюционного
моделирования с динамическими параметрами. // Информационные технологии. –
2001. – № 6. – С. 10-15.
6.
Тененев В.А., Якимович Б.А., Паклин Н.Б. Оптимальное управление детерминированными и нечеткими системами. // Вестник ИжГТУ. –
Ижевск: Изд-во ИжГТУ, 2003. – Вып. 1. – С. 35-40.
7.
Осовский С. Нейронные сети для обработки информации / Пер. с польского И.Д.Рудинского. – М.: Финансы и статистика, 2002.
– 344 с.