1. ВВЕДЕНИЕ
Алгоритмы мягкого декодирования блочных и сверточных кодов рассмотрены в работах [1, 2, 4, 5]. Их
действие часто сравнивается с функционированием аналогового фильтра, имеющего
на входе и выходе некоторые значения входных и выходных величин. Применение мягких
решений позволяет получить значительный выигрыш при декодировании блочных и сверточных кодов.
Однако на практике до недавнего времени в основном
находили применение алгоритмы Витерби [1], использующие
для декодирования мягкие решения демодулятора с жестким решением декодера. Это
объяснялось в первую очередь относительной простотой реализации данного типа
устройств на дискретных элементах. С развитием элементной базы, и в первую очередь
микропроцессорной техники расширились возможности использования такого рода алгоритмов.
Каскадные
коды являются одним из наиболее перспективных решений для повышения
достоверности принятой информации путем применения нескольких компонентных
кодеров, определенным образом соединенных между собой и обменивающихся
информацией о надежности принятой кодовой последовательности. В некоторых классах кодов обеспечивается циклическое
накопление информации о надежности по каждому принятому символу. Наиболее
яркими представителями данного класса являются турбокоды
[5] в которых используются компонентные кодеры с мягким входом и мягким выходом
(SISO) о которых пойдет речь далее.
2.
АЛГОРИТМЫ МЯГКОГО
ДЕКОДИРОВАНИЯ, ПРИМЕНЯЕМЫЕ В ТУРБОКОДАХ
А. Декодирование Витерби с мягким выходом (SOVA)
Это развитие классического алгоритма Витерби отличающееся от него получением на выходе
устройства его реализующего не только фиксированных значений декодированной
последовательности, а и значений надежности такого решения. Мягкое решение на
выходе декодера SOVA (алгебраическая
ценность решения) описывается выражением:
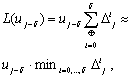 (1)
(1)
где 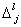 - усредненная разность
метрик l и j-ого
путей решетки. Применение SOVA
усложняет схему декодера Витерби на 70 – 80%.
- усредненная разность
метрик l и j-ого
путей решетки. Применение SOVA
усложняет схему декодера Витерби на 70 – 80%.
В. Алгоритмы
декодирования МАР
Алгоритмы максимума апостериорной вероятности (МАР) , иначе алгоритмы BCJR (Bahl, Coce,
Jelinek,
Raviv)
[3], разработаны для оценки вероятностных переходов наблюдаемых марковских цепей и применяется для декодирования сверточных и блоковых кодов. Основное их отличие от алгоритмов
Витерби заключается в том, что мягкое решение
принимается не по последовательности символов, а по каждому декодируемому
символу в отдельности. Подобные алгоритмы представлены в [1]. Следует подробнее
рассмотреть разновидности МАР, поскольку, несмотря на кажущуюся сложность, они
представляют наибольший интерес для построения схем итеративного декодирования,
так как позволяют не только оценивать надежность принятой последовательности,
но и принимать надежные решения в отношении каждого принятого символа.
Классический алгоритм МАР в упрощенном виде можно рассматривать как два
алгоритма Витерби, выполняемых навстречу друг другу с
разных концов принятого блока. Мягкое решение на выходе блока SISO-MAP
определяется как
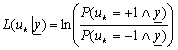 (2)
(2)
Сложность алгоритма в том, что для всех узлов решетки прямой
и обратной рекурсией должны быть вычислены вероятностные состояния. Данный
алгоритм обеспечивает выигрыш по сравнению с SOVA около 0,5 дБ, но требует больших
вычислительных затрат и большего объема памяти.
Max-log-MAP (ML-MAP) алгоритм основывается на
алгоритме МАР но значительно снижает его сложность, выполняя вычисления в логарифмической
области с аппроксимацией:
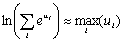 (3)
(3)
Такое приближение упрощает вычисления, однако проигрывает
МАР до 0,3 дБ в области низких соотношений сигнал/шум. Существенным недостатком
также является необходимость хранения в памяти первых значений рекурсивных
путей. Объем необходимой памяти будет зависеть от числа состояний кода и длины
блока. По сложности выполнения ML-MAP сопоставим
с SOVA [6].
Алгоритм Log-MAP (L-MAP)
выполняет вычисления подобно ML-MAP, а затем производится табличный
поиск и коррекция полученных значений. По качеству декодирования и сложности
сопоставим с классическим МАР.
Алгоритм МАР со скользящим окном (S-MAP) [7] лишен основного недостатка
других модификаций МАР – необходимости приема всего блока. Рекурсивные вычисления
выполняются на субблоках, сопоставимых по длине с
выживающей ветвью алгоритма Витерби. Поэтому значительно
уменьшается размер требуемой памяти. Недостатком S-MAP является увеличение объема вычислений в связи с тем, что для
каждого субблока необходимо точно вычислять начало
вектора обратной рекурсии.
Проведенный анализ
показывает, что для реализации равных по производительности декодеров сложность
и энергопотребление схем ML-MAP и S-MAP незначительно отличается от схем SOVA.
При применении параллельных вычислений объем их схем меньше SOVA до приблизительно 20%, и с
увеличением длины блока эта разница растет.
3. РЕАЛИЗАЦИЯ АЛГОРИТМОВ
МАР
Различные способы
реализации описаны в [8]. Организация вычислений алгоритмов МАР, работающих в
реальном масштабе времени является одной из важнейших задач построения устройств
декодирования. Архитектура выполнения алгоритмов влияет как на производительность
устройства, так и на его конструктивные особенности (сложность,
энергопотребление, массогабаритные показатели). При реализации алгоритмов МАР
приходится считаться в первую очередь с размером и конфигурацией требуемой
памяти, необходимой для хранения результатов прямой (Ak) и обратной
(Bk) рекурсии.
Также необходимо учитывать число этих рекурсий (nA, nB) и размер принимаемого блока (L). Этими параметрами будут определяться задержка декодирования
и вычислительная сложность. В табл. 1 представлены параметры некоторых известных
архитектур реализации МАР.
В ходе проведения
исследований определены возможные способы снижения вычислительной сложности
алгоритмов декодирования и объемов требуемой памяти. Так, например, при регулярном выкалывании проверочных символов
возможно со-
вместное хранение в виде единого массива в памяти ЦПОС
оценок нескольких выходов
систематических сверточных кодов. Например, в
распространенном случае применения параллельно объединенных сверточных
кодов со скоростью ½ и выкалыванием каждого второго проверочного символа
результирующий объем памяти данных необходимых на хранение принятых оценок
проверочных символов снижается вдвое.
Другие возможности снижения вычислительной сложности
алгоритма декодирования и снижения объема выделяемой памяти связаны с алгоритмом вычисления метрик априорной/апостериорной вероятностями приема
кодового символа, метрик состояний и переходов между ними.
Так, в частности, в BCJR алгоритме, для вычислении априорной (внешней) информации
поступающей на вход следующей ступени декодера из полученной оценки
апостериорной вероятности приема кодового символа извлекается часть связанная с априорной (внешней) информацией и информацией
полученной по систематическим символам поступившим на вход этой ступени. Эти
вычисления являются избыточными в случае если
систематическая часть передается однократно и оценки символов поступивших на
вход второй ступени получаются путем перемежения. В приведенном случае
достаточно лишь исключить внешнюю (априорную) информацию поступавшую на вход
данной ступени, остаток же, поступающий на вход
следующей ступени, будет представлять собой сумму внешней
информации и оценок
систематических бит.
Существенная экономия как
объема оперативной памяти, так и вычислительного ресурса может быть достигнута
за счет корректировки алгоритма вычисления оценок вероятностей переходов. В
частности, анализ показывает, что в случае применения выколотых кодов существенная
часть слагаемых, участвующих в вычислении оценок вероятностей переходов
является предопределенной и их вычисление может быть опущено без снижения
качества декодирования. По этой же причине является рациональным совместить вычисление
вероятностных метрик переходов с вычислением метрик состояний, а не использовать для этого отдельный блок
вычислений. Указанное, кроме того, позволяет отказаться
от хранения в памяти больших массивов данных
включающих метрики переходов.
И
наконец, наибольшую экономию позволят достичь совмещение процедур вычисления
одного из типов метрик состояний (α или β) с вычислением оценок апостерироных
вероятностей. Так, частные слагаемые при вычислении оценок апостериорных
вероятностей полностью совпадают с используемыми для вычисления одной из метрик
(α или β) в связи
с чем, во-первых, возможно существенно сократить объем вычислений, а во-вторых отказаться от хранения в памяти одной из метрик
состояний, массивы данных которой являются самыми большими при реализации алгоритмов
декодирования турбокодов.
4. ВЛИЯНИЕ ТОЧНОСТИ ПРЕДСТАВЛЕНИЯ ДАННЫХ
Как показали
проведенные исследования разрядность представления данных существенным образом
влияет как на сложность (при реализации на ПЭВМ или ЦПОС), так и на
качество декодирования. Применение параллельных вычислений за счет векторизации
при снижении разрядности способствует снижению вычислительной сложности, но
снижает и качество декодирования. Особенно сильно это проявляется в том случае,
если при нормировке метрик состояний и метрик апостериорной вероятности
используется жесткое ограничение оценок по максимальному значению являющемуся
стандартным в цифровой обработке сигналов. Такое ограничение проявляется в
связи с тем, что при каждой новой итерации декодирования исходные оценки полученные из канала связи играют всё меньшую роль,
так как получаемые на каждом новом цикле оценки апостериорной/априорной
информации увеличиваются по абсолютному значению и неизбежно выходят за рамки
ограниченной разрядной сетки. Гораздо более эффективным при решении задач
декодирования турбокодов является переход от жесткой
нормировки по максимальному значению к представлению чисел с фиксированной
точкой, позиция которой по мере необходимости меняется от итерации к итерации.
Это позволяет максимально сохранить наибольшее число значащих разрядов и на
ограниченной разрядной сетке получить максимальное качество декодирования.
Проведенные исследования показывают, что при 16-битном представлении данных
применение такого подхода позволяет получить энергетический выигрыш до 1 дБ по
отношению к жесткой нормировке по уровню, что существенно для турбокодов используемых в первую очередь при низких
соотношениях мощностей сигнала и шума.
5. ЗАКЛЮЧЕНИЕ
В докладе нами
представлен обзор наиболее перспективных алгоритмов мягкого декодирования и возможных
способов их аппаратной реализации. Полученные в ходе исследования результаты
позволяют надеяться на получение значительного выигрыша при декодировании
блочных и сверточных кодов, являющихся компонентными
кодами турбокодов, при снижении вычислительной
сложности и размера требуемой памяти, что в
конечном счете позволит расширить
диапазон их практического применения.
Литература
1. Дж. Кларк, мл, Дж Кейн, “Кодирование с исправлением
ошибок в системах цифровой связи”, М. “Радио и связь”, 1987, стр 140 –146, 216.
2. У. Питерсон, Э. Уэлдон, “Коды, исправляющие
ошибки”, М., “Мир”, 1976, стр. 449-455.
3. L. Bahl,
J. Cocke, F. Jelinek and J.
Raviv, “Optimal decoding of linear codes for minimising symbol error rate,” IEEE Transactions on
Information Theory, vol. IT–20, pp. 284–287, Mar. 1974.
4. J. Hagenauer, P. Hoeher, “A Viterbi algorithm with soft-decision outputs and its
applications”, Proc. GLOBECOM’89, Dallas, Texas, pp. 11-47, Nov. 1989.
5.
C. Berrou, A. Glavieux and
P. Thitimajshima, “Near Shannon limit
error–correcting coding and decoding: turbo–codes,” ICC 1993, Geneva,
Switzerland, pp. 1064–1070, May 1993
6. H. Dawid and H. Meyer, “Real-time algorithms
and VLSI architectures for soft output MAP convolutional
decoding," The Sixth IEEE International Symposium on Personal, Indoor and
Mobile Radio Communications (PIMRC), vol. 1, pp. 193-197, Sept. 1995.
7. J. Vogt, K. Koora, A. Finger and G. Fettweis “Comparison of different turbo decoder realizations
for IMT-2000” Proc. GLOBECOM’99, pp. 2704-2708 May, 1999.
8.
A.
Worm, H. Lamm, and N. Wehn,
“VLSI architectures for high-speed MAP decoders,” in 14’th Int. Conf. on VLSI design, 2001, pp. 446-453.
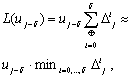 (1)
(1)![]() - усредненная разность
метрик l и j-ого
путей решетки. Применение SOVA
усложняет схему декодера Витерби на 70 – 80%.
- усредненная разность
метрик l и j-ого
путей решетки. Применение SOVA
усложняет схему декодера Витерби на 70 – 80%.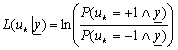 (2)
(2)![]() (3)
(3)